Курсовая работа: Проектирование модели для составления оптимального рациона кормления скота
4 . Проверяют уравнения на наличие единичного базиса и в те уравнения, где его нет вводятся искусственные переменные, т.е. коэффициенты при которых создают единичную матрицу, причем искусственные переменные нужно вводить со знаком «плюс».
Эти переменные вводятся также в целевую функцию с большими по абсолютной величине коэффициентами «М».Значение «М» можно за раннее задавать.
При решении задач искусственные переменные должны быть введены из оптимального варианта плана. Следовательно, никакого экономического смысла эти коэффициенты не имеют.
При решении задач на максимум в целевую функцию искусственные переменные вводятся с отрицательными коэффициентами «М».
При решении задач на минимум в целевую функцию искусственные переменные вводятся с положительными коэффициентами «М».
5. Построение первого опорного плана и заполнение первой строки zj -cj, которая вычисляется так:
z0 =![]() (графа С* графу вi ) (3.4)
(графа С* графу вi ) (3.4)
zj -cj =![]() (графа С* коэффициент аij )-cj (3.5)
(графа С* коэффициент аij )-cj (3.5)
6. Заполнение строки «М»
Будем считать, что коэффициент «М»=1, следовательно
![]() (графа С (М) * графу вi ) (3.6)
(графа С (М) * графу вi ) (3.6)
7. Проверка плана на оптимальность.
Если задача на max, то элементы индексной строки «М» должны быть неотрицательными. Если же хотя бы одна М меньше нуля, то план можно улучшить.
Бывает исключение, если в М – строке (на мах) все положительные элементы, то мы поднимается на строку Zj-Cj и выбираем максимальное отрицательное число.
Если задача на min, то М≤0. Если хоть одна разность больше нуля, то план можно улучшить.
Исключение, если в М – строке (на min) все отрицательные элементы, то мы поднимается на строку Zj-Cj и выбираем максимальное положительное число.
8. Выбор разрешающего столбца.
Если задача на max, то среди отрицательных М выбирается наибольшая по модулю.
Если задача на min, то среди положительных М выбирается наибольшая по модулю.
9. Выбор разрешающей строки.
Находим отношение графы «План вi» к положительным элементам разрешающего столбца и среди них находим минимальное, которое соответствует разрешающей строке. Если же минимальных отношений несколько, то за разрешающую выбирается меньшая по номеру строки, т.е. определили переменную, выводимую из базиса;
10. Выбор разрешающего элемента, находящегося на пересечении разрешающего столбца и строки;
11. Построение следующего опорного плана.
При выводе из базиса элементов с коэффициентом «М», исключаем данный столбец из плана, после чего переносим разрешающую строку путём деления её элементов на разрешающий элемент. При этом вводится новая переменная, соответствующая разрешающему столбцу. Все элементы графы «План bi» и коэффициенты aij определяются по правилу прямоугольника:
| akp ….. | akj | |
| aip ….. | aij | Разрешающая строка |
| Разрешающий столбец |
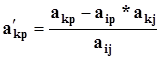 (3.7)
(3.7)
12. Проверка нового опорного плана на оптимальность.
Так повторяется до тех пор, пока полученный план не будет оптимальным; или задача не имеет решений. После этого записывается ответ из графы «План вi».
4 РЕШЕНИЕ ПОСТАВЛЕННОЙ ЗАДАЧИ
4.1 Условие задачи
В состав рациона кормления входят три продукта: сено, силос и концентраты, содержащие питательные вещества: белок, кальций, витамины. Содержание питательных веществ соответствующего продукта питания и минимально необходимые нормы их потребления заданы таблицей:
Таблица 4.1
| Продукты | Питательные вещества | ||
| Белок | Кальций | Витамины | |
| Сено | 50 | 6 | 2 |
| Силос | 20 | 4 | 1 |
| Концентраты | 180 | 3 | 1 |
| Нормы потребления | 2000 | 120 | 40 |