Курсовая работа: Проектирование оптимальных структур активных RC-фильтров

1. Базовая структура нестационарных устройств

Важным классом современных устройств автоматики, технической диагностики и техники специальных измерений являются нестационарные блоки и подсистемы, обеспечивающие обработку сигналов в реальном масштабе времени. Такие наблюдатели, оцениватели и фильтры достаточно часто строятся на базе сигнальных процессоров и воспроизводят непосредственно систему дифференциальных уравнений, вытекающую из основных процессов. Внедрение в инженерную практику объектов микросистемной техники, создание новых версий систем управления, обеспечивающих работоспособность объектов в критических ситуациях, связано с разработкой нового поколения высокоточных и экономичных нестационарных устройств.

Результаты показывают, что перестраиваемые ARC-фильтры с собственной компенсацией обеспечивают существенное повышение точности преобразования сигнала при невысоких требованиях к частоте единичного усиления активных элементов и, следовательно, низкой потребляемой мощности. Таким образом, объединение в единую систему экономичного микроконтроллера с развитой архитектурой портов ввода/вывода и ARC-фильтра с цифроуправляемыми параметрами теоретически позволяет решить сформулированную задачу (рис. 1). В приведенной структуре микроконтроллер вырабатывает управляющие воздействия на ARC-схему с цифроуправляемыми параметрами и контролирует процесс оценки координат объекта. В частном случае, когда управляющие слова могут быть определены заранее, многоканальный АЦП может отсутствовать, и микроконтроллер работает в режиме логического управления под действием внутреннего таймера.

С точки зрения принципа обработки входных аналоговых сигналов такую систему уместно назвать гибридной.

Методики, разработанные для исследований и анализа процессов, протекающих в нестационарных цепях, как известно, достаточно сложные. В общем случае для анализа применяют двухмерные преобразования Лапласа, теорию уравнений Хилла, а также различные спектральные методы. Достаточно важными результатами в области анализа линейных нестационарных систем, получившими распространение в радиотехнических цепях, являются работы Л.А. Заде. Необходимо отметить, что в радиотехнике большое развитие получили в основном методы анализа нестационарных цепей с периодически изменяющимися коэффициентами. В случае анализа нестационарных систем с непериодическими параметрами обычно пользуются приближенными методами и оценками. По аналогии с линейными стационарными системами в нестационарных определяющими являются понятия сопряженной импульсной переходной характеристики и параметрической передаточной функции. Первая показывает реакцию предварительно невозбужденной («пустой») нестационарной системы в момент времени приложения единичного импульса и является функцией двух переменных – . Вторая является изображением по Лапласу отношения выходной реакции системы к ее входу в момент времени t и также является функцией двух переменных – .

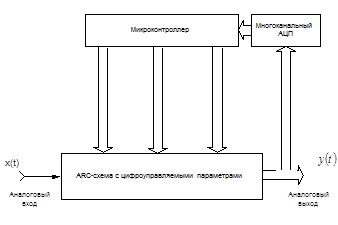
Рис. 1. Структура нестационарных ARC-устройств

Ограничимся линейной версией системы, когда любое воздействие может быть пересчитано к одному из ее входов. Следовательно, система линейных уравнений n-го порядка, описывающая нестационарное устройство, может быть представлена в виде следующего дифференциального уравнения с нестационарными коэффициентами:

,(1)

где m£n; – одна из выходных координат рассматриваемой системы; – приведенное эквивалентное входное воздействие, учитывающее скалярные сигналы аналоговой части, которое в символической операторной форме можно представить следующим образом:

, (2)

где ;

где ;

;

.

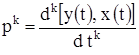Как показано в [2], с учетом (2) параметрическую передаточную функцию можно определить из решения следующего дифференциального уравнения:

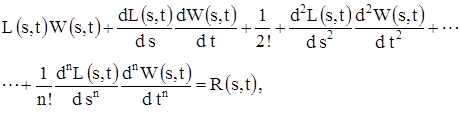(3)

где , .

Следуя [2], приведем методику приближенного определения параметрической передаточной функции (3), идея которой принадлежит Л.А. Заде. Перепишем (3) в следующем виде:

, (4)

где .

Решение отыскивается в виде ряда

, (5)

где – «замороженная» передаточная функция ФКБ, .

В работе [5] отмечается, что ряд (5) хорошо сходится только в случае медленно изменяющихся коэффициентов и . Однако быструю сходимость ряда можно обеспечить, выполняя построение функции на ограниченных интервалах времени, где функциональные зависимости и можно аппроксимировать полиномами низкого порядка.

Создание нестационарных устройств в рамках экономичных и быстродействующих структур предполагает обработку сигнала аналоговым способом с применением для указанной цели ARC-схемы с цифроуправляемыми параметрами. В такой постановке задачи необходимо говорить о дискретно-непрерывной фильтрации. Очевидно, что максимального приближения характера поведения дискретно-непрерывной и непрерывной систем можно добиться, уменьшая интервал дискретизации, верхняя граница которого может быть определена из теоремы Котельникова, однако при этом возрастают требования предъявляемые к производительности цифровой части устройства.

Необходимо отметить, что параметры цифроуправляемой ARC-схе-мы на интервале времени, определяемом частотой дискретизации, остаются постоянными, то есть параметрическая передаточная функция (5) совпадает с передаточной функцией стационарной схемы при замораживании в ней на -м шаге коэффициентов

, (6)

где ;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--