Курсовая работа: Проектирование системы оптимального корректирующего устройства

Рис. 1.17. АФЧХ разомкнутой системы

Так как годограф Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывает особую точку (−1;j0), то замкнутая система устойчива.

Из рис. 1.17 видно, что годограф скорректированной системы наиболее удален от особой точки (−1;j0), следовательно, имеет наибольшие запасы устойчивости в отличие от системы с пропорциональным регулятором.

Построим годограф Михайлова замкнутой системы (см. п.1.2.2).

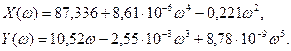
Годограф Михайлова изображен на рис. 1.18 по характерным точкам (табл. 1.9):

Таблица 1.9

ω
0	87,336	0
20,037	0	190,39
64,71	-687,1	0
158,94	0	-7673
534,97		0

Так как годограф системы, имеющей пятый порядок, при изменении ω от 0 до ∞, начинается на вещественной положительной полуоси и при увеличении ω в положительном направлении последовательно проходит пять квадрантов, и при этом не обращается в 0, то можно сделать вывод, что система устойчива.

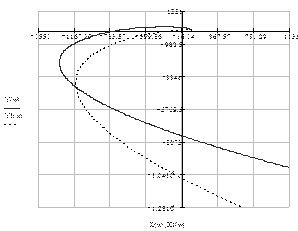
Рис. 1.18. Годограф Михайлова (справа увеличен в начале координат)

1.4.2 Определение частотных ПК, запасов устойчивости, критического коэффициента усиления