Курсовая работа: Проектування офісу по ремонту ЕОМ

Рисунок 2.18 – Пошук рішення

Необхідний кут θ дорівнює 66 градусів.

Рішення засобами MathCAD

Для рішення у MathCAD необхідно задатися початковими значеннями:

З використанням функції Maximize знаходимо оптимальний обсяг конуса.

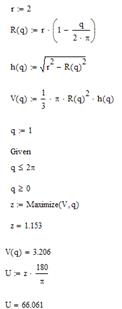
Рисунок 2.19 – Розв’язання в MathCAD

Результат : кут θ дорівнює 66 градусів.

Дане рівняння вирішили різними методами й засобами в результаті одержали однакові відповіді, але методи рішення відрізняються. Тому що за допомогою програми MathCAD неможливо зрозуміти процес рішення задачі, що дозволяє зробити MS Excel.

Задача Б. Проектування 2 -х конусоподібних (пожежних) ребер.

З круглої заготівлі жерсті (r = 3 ) вирізають сектор з кутом , потім з іншого роблять цебро у виді конуса і з вирізаного сектора теж (тобто 2-а цебра) (рис.2.20).

Необхідно розрахувати величину кута , тобто як необхідно розкроїти заготівлю, щоб обсяг 2-х цебер був максимальним.

R – радіус основи конуса; h – висота конуса; r – радіус заготівлі.

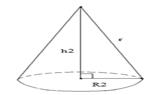
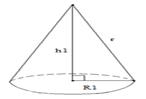
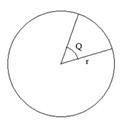
Рисунок 2.20 – Окружність, велика заготівля, маленька заготівля

Формули для знаходження радіусу R, висоти h та обсягу V великої заготівлі:

Формули для знаходження радіусу R, висоти h та обсягу V маленької заготівлі:

Цільова функція має вид:

Обмеження:

Розв’язання засобами Excel