Курсовая работа: Пространства Соболева
Доказательство. Пусть ![]() тогда для всех
тогда для всех ![]() имеем (1.6):
имеем (1.6):
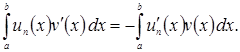
Вследствие свойства непрерывности скалярного произведения в последнем равенстве можно перейти к пределу при ![]() В результате мы получим тождество (1.6) для любой функции
В результате мы получим тождество (1.6) для любой функции ![]() Лемма доказана.
Лемма доказана.
Лемма 2. Пусть даны ![]()
![]() такие, что для всех
такие, что для всех ![]() справедливо тождество (1.7). Тогда
справедливо тождество (1.7). Тогда ![]() (обобщённая производная).
(обобщённая производная).
Доказательство. Пусть ![]() а
а ![]() Тогда
Тогда
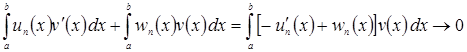 при
при ![]()
для любого ![]()
Пусть ![]() – класс, представителем которого является
– класс, представителем которого является ![]()
Тогда 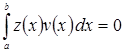 для любых
для любых ![]() Отсюда
Отсюда ![]() Лемма доказана.
Лемма доказана.
1.4 Простейшая теорема вложения
Теорема 1. ![]() вложено в
вложено в ![]()
Доказательство. Пусть ![]() непрерывно дифференцируема на отрезке
непрерывно дифференцируема на отрезке ![]() Согласно теореме о среднем, вследствие непрерывности
Согласно теореме о среднем, вследствие непрерывности ![]() найдётся точка
найдётся точка ![]() такая, что
такая, что  Поэтому на отрезке
Поэтому на отрезке ![]() справедливо следующее тождество:
справедливо следующее тождество:

С помощью неравенства Коши-Буняковского имеем

где  Следовательно, для любой непрерывно дифференцируемой на отрезке
Следовательно, для любой непрерывно дифференцируемой на отрезке ![]() функции
функции ![]() справедливо неравенство
справедливо неравенство
![]() (1.8)
(1.8)
Пусть теперь последовательность ![]() – фундаментальная по норме
– фундаментальная по норме ![]() Тогда
Тогда
![]()
при ![]() Следовательно,
Следовательно, ![]() фундаментальна в смысле равномерной сходимости и, по критерию Коши равномерной сходимости, сходится к
фундаментальна в смысле равномерной сходимости и, по критерию Коши равномерной сходимости, сходится к ![]() Тем более
Тем более ![]() в среднем. Таким образом, в классе из
в среднем. Таким образом, в классе из ![]() содержащим
содержащим ![]() в качестве представителя, содержится непрерывная функция
в качестве представителя, содержится непрерывная функция ![]() и, значит, этот класс можно отождествить с
и, значит, этот класс можно отождествить с ![]() Отождествим элементы
Отождествим элементы ![]() с непрерывными функциями. Пусть
с непрерывными функциями. Пусть ![]() Переходя в неравенстве
Переходя в неравенстве ![]() к пределу при
к пределу при ![]() придём к неравенству (1.8).
придём к неравенству (1.8).
Итак, вложение ![]() в
в ![]() доказано. Доказательство теоремы закончено.
доказано. Доказательство теоремы закончено.
1.5 Пространства Соболева  и
и 
Пусть ![]() – односвязная область с достаточно гладкой границей
– односвязная область с достаточно гладкой границей ![]() В замкнутой области
В замкнутой области ![]() рассмотрим линейное пространство всевозможных непрерывно дифференцируемых функций
рассмотрим линейное пространство всевозможных непрерывно дифференцируемых функций ![]() со скалярным произведением
со скалярным произведением

При этом
 (1.9)
(1.9)
Полученное пространство со скалярным произведением обозначается ![]() а его пополнение – это, по определению, пространство Соболева
а его пополнение – это, по определению, пространство Соболева ![]()
Пусть ![]() – фундаментальная последовательность в
– фундаментальная последовательность в ![]() то есть
то есть ![]() при
при ![]() Отсюда следует, что в
Отсюда следует, что в ![]() будут фундаментальными последовательности
будут фундаментальными последовательности

Вследствие полноты ![]() в
в ![]() имеются элементы, которые мы обозначим
имеются элементы, которые мы обозначим

так что при ![]() в среднем
в среднем
