Пространства Соболева и тесно связанное с ним понятие обобщённой производной в смысле Соболева были введены в математическую практику академиком С.Л. Соболевым и играют важнейшую роль в теоретических и прикладных вопросах математической физики и функционального анализа. Пополнение пространства гладких функций некоторыми идеальными элементами, которые можно с любой степенью точности вычислить с помощью элементов из приводит, с одной стороны, вследствие полноты к точности и завершённости многих математических утверждений, а с другой стороны, сохраняет все вычислительные возможности.

1. Пространства Соболева

1.1 Общее определение

Пусть в задана замкнутая ограниченная область Рассмотрим линейное пространство вещественных функций раз непрерывно дифференцируемых на Дифференцируемость на замкнутой области можно понимать в различных смыслах. Мы будем предполагать, что в функции раз непрерывно дифференцируемы, причём каждая частная производная функции имеет предел при стремлении к любой граничной точке области так что в результате её продолжения на она становится непрерывной в Граница области предполагается достаточно гладкой. Кроме того, обычно мы будем считать область односвязной и удовлетворяющей таким дополнительным ограничениям, которые могут понадобиться в тех или иных рассуждениях.

Воспользуемся для краткости следующими обозначениями. Набор индексов называется мультииндексом. Число называется длиной мультииндекса. Для обозначения частных производных примем

Введём в рассмотренном выше линейном пространстве норму

(1.1)

Полученное нормированное пространство обозначается Его пополнение в норме (1.1) обозначается и называется пространством Соболева.

В прикладных задачах довольно часто встречается случай Общепринято следующее обозначение: Пространство Соболева является гильбертовым пространством – пополнением пространства в норме, порождённой скалярным произведением

Ниже мы подробнее остановимся на частных случаях и то есть рассмотрим пространства Соболева на вещественной оси и в трёхмерном пространстве.

1.2 Пространство

Рассмотрим на отрезке пространство состоящее из всевозможных функций непрерывно дифференцируемых на со скалярным произведением

(1.2)

и соответствующей этому скалярному произведению нормой

(1.3)

является пополнением в этой норме. Элементами согласно теореме о пополнении, являются классы, состоящие из последовательностей фундаментальных в в среднем, точнее, таких, что

при

Две такие последовательности и принадлежат одному классу, если является бесконечно малой по норме то есть, если

при

Из условия фундаментальности в среднем в следует, что отдельно при

Аналогично, из условия эквивалентности и по норме следует, что при

Согласно определению пространства существуют функции и такие, что при а в среднем.

Мы приходим к следующему важнейшему определению. Пусть Тогда в определены элемент с представителем и элемент с представителем называется обобщённой производной (в смысле Соболева) от При этом пишут:

Из определения обобщённой производной видно, что она определяется не локально, в отдельных точках, а глобально – сразу на всём отрезке Пусть так что Перейдём к пределу при в равенствах

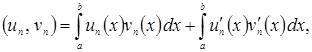(1.4)

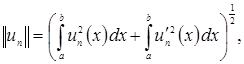(1.5)

и, согласно теореме о пополнении и определению интеграла Лебега, придём к формулам (1.2) и (1.3), где теперь производные понимаются в обобщённом смысле, а интеграл – в смысле Лебега. Для конкретных вычислений, разумеется, можно и нужно пользоваться формулами (1.4) и (1.5), взяв достаточно большое то есть вместо идеальных элементов воспользоваться их гладкими приближениями

1.3 Другое определение обобщённой производной

Пусть – множество всех непрерывно дифференцируемых на отрезке финитных функций Если теперь непрерывно дифференцируема на отрезке то для произвольной функции справедливо следующее интегральное тождество:

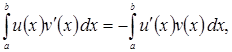(1.6)

проверяемое интегрированием по частям. Этим тождеством полностью определяется.

Допустим, что, кроме того, для любых и некоторой непрерывной на отрезке функции

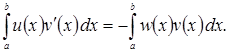(1.7)

Вычитая эти тождества, получим, что для любых

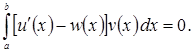
Отсюда, вследствие плотности в на отрезке Оказывается, интегральное тождество (1.7) можно принять за определение обобщённой производной. Прежде всего, справедлива следующая лемма.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--