Курсовая работа: Пространства Соболева
Скалярное произведение и норма задаются в 
теми же формулами, что и в 
в которых теперь производные обобщённые, а интегрирование понимается в смысле Лебега. Введем в рассмотрение пространство 
Это пространство является пополнением в норме
(1.10)
линейного пространства функций, непрерывно дифференцируемых на 
и таких, что 
является гильбертовым пространством со скалярным произведением
Лемма 3. Если 
а 
то
Доказательство. Достаточно доказать первую из этих формул. Она справедлива, если 
а 
Пусть 
– фундаментальная в 
последовательность, предел которой – элемент 
Переходя в тождестве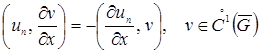 
к пределу при 
получим для любой Действительно, из сходимости в 
следует, что
то есть непрерывность скалярного произведения.
Пусть теперь 
– фундаментальная последовательность в 
Перейдём к пределу в тождестве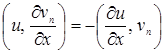 
и получим исходное тождество.
Следствие. содержится строго внутри 
Действительно, функция 
Но 
иначе мы имели бы 
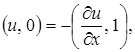то есть 
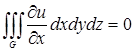для любой Возьмём 
и получим противоречие.
Теорема 2 (Фридрихс). Существует постоянная 
такая, что для любых 
Доказательство. По самому определению всякий элемент из принадлежит 
Пусть 
и сходится в к
Построим куб 
содержащий область 
Функции 
доопределим нулём в 
Частная производная 
существует всюду в 
за исключением, быть может, тех точек, в которых прямая, параллельная оси абсцисс, пересекает границу 
области 
Для любой точки 
имеем
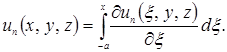
По неравенству Коши-Буняковского
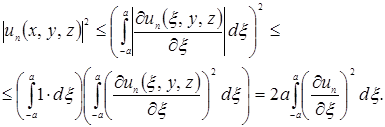
Интегрируя полученное неравенство по находим
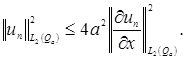
Так как 
вне 
то
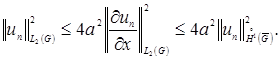
Переходя к пределу при приходим к доказываемому неравенству Фридрихса.
Следствие 1. Пространство вложено в
Это предложение непосредственно вытекает из определения вложения банаховых пространств и неравенства Фридрихса.
Следствие 2. В нормы (1.9) и (1.10) эквивалентны.
Действительно, используя неравенство Фридрихса, имеем
