Курсовая работа: Процедура расчета и создания стержней с заданными характеристиками
1 вариант:
 мм
мм
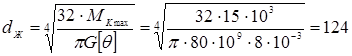 мм
мм
Следовательно, d1 = max {dпч,dж} = 124 мм. Принимаем по ГОСТ 6636-86 d1 = 130 мм. Жесткость поперечного сечения данного вала равна
![]() МН·м2
МН·м2
2 вариант:
 мм
мм
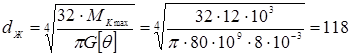 мм
мм
Следовательно, d2 = max {dпч,dж} = 118 мм. Принимаем по ГОСТ 6636-86 d2 = 120 мм. Жесткость поперечного сечения данного вала равна
![]() МН·м2
МН·м2
Требуемый диаметр вала по второму варианту получается меньше, чем по первому. Тем самым переход от заданного расположения шкивов к рациональному приводит к экономии материала, равной

Построение эпюры угла закручивания φ.
Угол поворота определяется по формуле
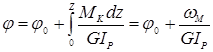
где φ0 – угол поворота в начале участка;
ωМ – площадь эпюры крутящего момента от начала участка до рассматриваемого сечения.
Так как крутящий момент остается постоянным в пределах каждого участка, то согласно первой формуле угол φ меняется по линейному закону. Вычисляем углы поворота на границах участков и строим эпюры (рис.4,в и рис.5,в)
1 вариант:
φ0 = φА = 0
 мрад
мрад
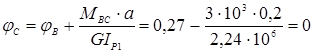 мрад
мрад
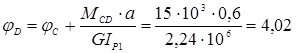 мрад
мрад
2 вариант:
φ0 = φВ = 0
 мрад
мрад
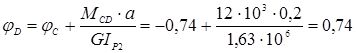 мрад
мрад
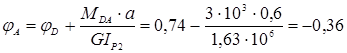 мрад
мрад
3 Процедура создания стержней
3.1 Создание стальной балки
Спроектировать стальную балку (рис. 6,а) в 5 вариантах поперечного сечения: круглого, прямоугольного (h/b=2), двутаврового, из швеллеров и уголков, приняв допускаемое напряжение [σ] = 160 МПа. Оценить экономичность всех пяти сечений и начертить их в одном масштабе. Для балки двутаврового профиля построить эпюры нормальных и касательных напряжений, а также исследовать аналитически и графически напряженное состояние в точке К опорного сечения.
Принять: М = 4qa2 кН·м, F = 2qa кН, q=15 кН/м, а = 1,2 м, yк /h= – 0,1
Решение
1. Определение опорных реакций и построение эпюр Qy и Mx.
ΣYi=0
RA - 2qa + q2a = 0
RA =4qa
ΣmA=0
MA - 4qa2 + 2qa3a-q2a2a = 0
MA = 4qa2 + 6qa2 + 4qa2 = 14qa2
ЭпюраQy. Строится по формуле
Q = Q0 ± qz
В данном случае следует взять знак «минус», так как погонная нагрузка направлена вниз. Поперечная сила постоянна на участке АВ (q=0) и изображается наклонной прямой на участке MF (q=const). Вычисляем значения Qyв характерных точках и строим ее эпюру (рис. 6,б)
QA=RA=4qa
QAB=QA=4qa
QBC=QAB – q2a=4qa – 2qa=2qa
QC =QBC – 2qa=2qa – 2qa=0
Эпюра Mx. Строится по формуле
Mx = M0 + Q0Z – 0,5qz2
Изгибающий момент изменяется по квадратичному закону на участке MF (q=const) и по линейному закону – на участке АВ (q=0). Вычисляем значения в характерных точках и строим эпюру (рис. 6,в)
MA = – 14qa2
MAВ = MA + 4qa2 = – 14qa2+ 4qa2 = – 10qa2
MВ = MAВ + 4qa2 = – 10qa2+ 4qa2 = – 6qa2
MВС = MВ + 6qa2 = – 6qa2+ 6qa2 = 0
Расчетный изгибающий момент равен
Mрас = |MA| = 14qa2 = – 14·15·103·1,2 = 302,4 кН·м
Подбор сечений.
Из условий прочности по нормальным напряжениям определяем требуемый момент сопротивления поперечного сечения по кторому подбираем конкретные сечения

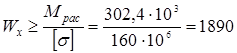 см3
см3
Круг:
![]()
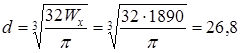 см
см
Принимаем по ГОСТ 6636-86 нормализованное значение d0=270 мм, тогда
![]() см3
см3
Прямоугольник (h/b=2):
![]()
 см
см
Ближайшее меньшее стандартное значение равно b0=140 мм. При этом балка будет работать с перенапряжением, равным
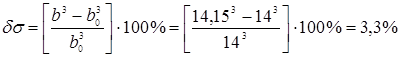
что удовлетворяет требованию, и для которого
![]() см2
см2
Двутавр. По ГОСТ 8239-89 выбираем двутавр № 55 для которого ![]() =2035 см3, A3=118 см2.
=2035 см3, A3=118 см2.