Курсовая работа: Процедура расчета и создания стержней с заданными характеристиками
Неравнобокие уголки. Они находятся подбором, так как в сортаменте не даны значения момента сопротивления. Использую формулу
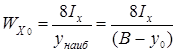
Сделав несколько попыток, выбираем восемь уголков 250´160´16 для которых
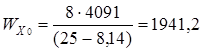 см3
см3
A5=8·63б6=508,8 см2
Оценка экономичности подобранных сечений
Масса балки определяется как произведение плотности материала на ее объем m=rAl , т.е. расход материала при прочих равных условиях зависит только от площади поперечного сечения А. Сравнивая массы балок
m1 : m2 : m3 : m4 : m5 = A1 : A2 : A3 : A4 : A5 = 1 : 0,68 : 0,2 : 0,28 : 0,89 заключаем, что самым неэкономичным является круглое сечение. При замене круга другими формами (прямоугольник, двутавр, три швеллера, восемь уголков) достигается экономия, равная соответственно 32%, 80%, 72% и 11%.
Исследование напряжений в опорном сечении для балки двутаврового профиля № 55 (рис. 7,а), параметры которой по ГОСТ 8239-89 равны:
h=55 см, b=18 см, d=1,1 см, t=1,65 см, Ix=55962 см4, Sx=1181 см3
Внутренние силовые факторы в опорном сечении А:
QA = 4qa=4·15·1,2 = 72 кН
MA = – 14qa2 = – 14·15·103·1,22 = – 302,4 кН·м
Эпюра σ. Нормальные напряжения в поперечном сечении изменяются по линейному закону
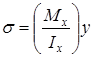
Вычисляем напряжения в крайних точках и строим эпюру σ (рис. 7,б)
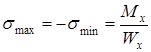
Эпюра τ. Она строится по формуле Журавского

Находим значения τ в 4 характерных точках по высоте сечения (необходимые вычисления представлены в табл. 3) и строим касательные напряжения (рис. 7,в)
Таблица 3 – Вычисления касательные напряжений в характерных точках
| № точек | bi,мм | |||||
| 1,1΄ | 18 | 0 | 0 | 0 | 0 |
|
| 2,2΄ | 18 | 792 | 44 | 0,04 | 0,6 | |
| 3,3΄ | 1,1 | 792 | 720 | 0,7 | 9,3 | |
| 4 | 1,1 | 1181 | 1073,6 | 1 | 14 |
Определение главных напряжений в точке К (yк /h= – 0,1):
– напряжение в поперечном сечении
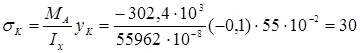 МПа
МПа
 МПа
МПа
– величины главных напряжений
![]()
σ1 = 35,25 МПа
σ3 = – 5,25 МПа
– ориентация главных площадок

![]() 21º
21º
Экстремальные касательные напряжения равны по величине
![]() МПа
МПа
и действуют на площадках, равнонаклоненных к осям 1 и 3.
3.2 Выбор материала
Согласно схеме нагружения (рис. 9,а), подобрать сечение балки (рис. 10), изготовленной из материала, неодинаково работающего на растяжение и сжатие.
Принять: М = 4qa2 кН·м, F = 2qaкН, q= 15 кН/м, а = 1,2 м,
[σр] = 40 МПа, [σс] = 70 МПа
Решение
1. Определение опорных реакций и построение эпюр Qx и Mx.
ΣmB=0
RA4a - 2qaa - 4qa2- q3a3,5a = 0
RA = 4,125qa
ΣYi=0
RA - 2qa - q3a+ RB = 0
RB =0,875qa
Эпюра Qy. Строится по формуле
Q = Q0 ± qz
В данном случае берем знак «минус», так как погонная нагрузка направлена вниз. Находим значения поперечной силы в характерных точках и строим ее эпюру (рис. 9,б)
QС = 0
QCA = QC–qa= – qa
QA = QCA + RA = – qa + 4,125qa = 3,125qa
QAF = QA – 2qa = 3,125qa – 2qa = 1,125qa
QFD = QAF= 1,125qa
QD = QFD – 2qa = 1,125qa – 2qa = – 0,875qa
QDB = QD= – 0,875qa
QB = QDB + RB = – 0,875qa + 0,875qa = 0
Эпюра Mx. Строится по формуле
Mx = M0 + Q0Z – 0,5qz2
Изгибающий момент изменяется по квадратичному закону на участке CA и AF (q=const) и по линейному закону – на участках FD и DB (q=0). Вычисляем значения в характерных точках и строим эпюру (рис. 9,в)
MС = –4qa2
MA = MС – 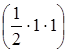 qa2 = – 4qa2 – 0,5 = – 4,5qa2
qa2 = – 4qa2 – 0,5 = – 4,5qa2
MF = MA + 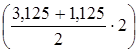 qa2 = – 10qa2+ 4qa2 = – 6qa2
qa2 = – 10qa2+ 4qa2 = – 6qa2
MD = MF + 1,125qa2 = – 0,25qa2+ 1,125qa2 = 0,875qa2
MB = MD – 0,875qa2 = 0,875qa2+ 0,875qa2 = 0
Расчетный изгибающий момент равен
Mрас = |MA| = 4,5qa2 = 4,5·15·103·1,22 = 97,2 кН·м
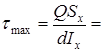
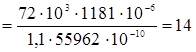 МПа
МПа