Курсовая работа: Процесс создания математической модели объекта
W(jw)=![]()
![]()
По полученному выражению получаем значения для построения АЧХ, ФЧХ и АФЧХ. Для этого вновь воспользуемся программой MSExcel для удобства проведения громоздких расчетов (Таблица значений АЧХ и ФЧХ приведена в приложении). График АФЧХ – есть зависимость Im(Re). По полученным значениям и по виду графика можно видеть, как меняется данная зависимость.
По полученным графикам можно сделать вывод, что данное звено является фильтром низких частот. Оно пропускает амплитуду сигнала на более низких частотах. На высоких частотах это пропускание стремится к нулю. Об этом говорит график АЧХ. График ФЧХ показывает то, что с увеличением частоты подаваемого на вход сигнала, происходит снижение рассогласования фаз выходного и входного значений сигнала. АФЧХ, в свою очередь, имеет интересный вид. График пересекает единичную окружность дважды, и стремится к нулю. Если в случае замкнутой системы это говорит о ее устойчивости по Ляпунову, то в случае разомкнутой это также говорит об устойчивости. Данное утверждение подтверждает и вид переходной характеристики, построенной при помощи пакета VisSim30 (графики АЧХ, ФЧХ, АФЧХ и график переходной характеристики полученного звена приведены в приложении).
3.По заданному закону регулирования найти математическую модель ЗСАУ.
Используя заданный ПИД–регулятор, необходимо найти математическую модель замкнутой системы автоматического управления (ЗСАУ). ПИД – закон имеет следующие заданные параметры и вид передаточной функции:
ПИД – Кп = 0,8 Ки = 0,1 Тд = Кд = 10

Составим структурную схему данной САУ:

ПИД W(P)
Описание работы системы: управляющий сигнал подается на вход регулятора. Регулятор преобразует входной сигнал и преобразованный по своему закону сигнал подает на вход объекта регулирования. Выходной сигнал вновь подается на вход системы, но только на, так называемое, устройство сравнения, и с учетом полученной разности выходного сигнала подается на вход регулятора.
С учетом структуры системы определим передаточную функцию ЗСАУ. Для удобства сначала определим WРСАУ (P) с учетом передаточной функции имеющегося регулятора, а потом запишем передаточную функцию ЗСАУ .
![]()
передаточная функция замкнутой системы будет иметь вид:
![]()
(График переходной характеристики приведен в приложении)
4.Определение устойчивости ЗСАУ.
Составление математической модели системы является важным этапом математического моделирования. Но также не маловажным условием полученной модели является ее устойчивость. Для избежания неблагоприятных последствий во время эксплуатации систем, на стадии моделирования обязательной стадией исследования является исследование модели системы на устойчивость. Для определения устойчивости имеются несколько критериев, названных в честь их создателей: Найквиста, Михайлова, Рауса, Гурвица, Ляпунова. Позднее критерий Гурвица стали называть критерием Рауса – Гурвица, т.к. их способы несколько различаются, но принцип определения идентичен, в обоих случаях для нахождения устойчивости определяется матрица коэффициентов.
В связи с тем, что критерии Найквиста, Михайлова и Ляпунова являются корневыми методами, а мы имеем дело с передаточной функцией 4-го порядка, то для упрощения определения устойчивости воспользуемся критерием Рауса – Гурвица, который не требует нахождения корней.
Теорема Гурвица утверждает, что для того, чтобы действительные части всех корней характеристического уравнения (знаменателя передаточной функции)
![]()
c действительными коэффициентами и b0 >0 были отрицательными, необходимо и достаточно, чтобы были положительными все определители D1, D2, ..., Dm, составленные из коэффициентов уравнения по следующей схеме:
309808 математическая модель метод площадь
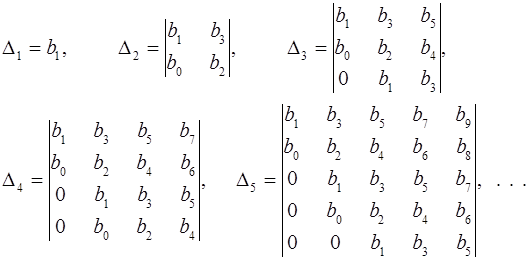 и т. д.
и т. д.
При составлении определителей по указанной схеме, коэффициенты с индексом, превышающим степень характеристического уравнения, заменяют нулями.
Согласно критерию Рауса – Гурвица, найдем определители характеристического уравнения ЗСАУ:
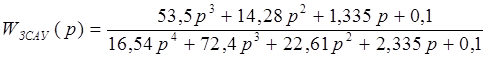
Характеристическое уравнение имеет вид:
![]()