Курсовая работа: Процесс создания математической модели объекта

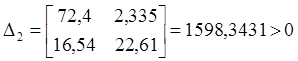
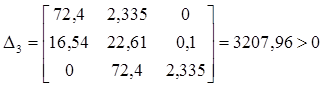
D₄ = 0,1*D₃ > 0

Так как все определители положительны, то согласно критерию устойчивости Гурвица, замкнутая система автоматического управления является устойчивой.

5. Нахождение переходной функции ЗСАУ и основных ПКР.

Нахождение переходной характеристики ЗСАУ возможно провести двумя способами: решение ДУ классическим методом или методом обратного преобразования Лапласа.

Решим одним из способов (обратным преобразованием Лапласа) полученную передаточную функцию ЗСАУ.

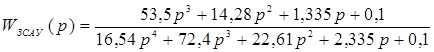
Для начала найдем все возможные корни данного уравнения, воспользовавшись численным методом нахождения корней.

р₁ = -4,048, р₂ = -0,1878.

Для нахождения оставшихся 2 комплексных корней разделим характеристическое уравнение на квадратный трехчлен, полученный путем умножения двух найденных корней. Разделив, получим корни:

р_3,4, = -0,071 ±j0,054

Перепишем исходное уравнение в виде и произведем необходимые вычисления:

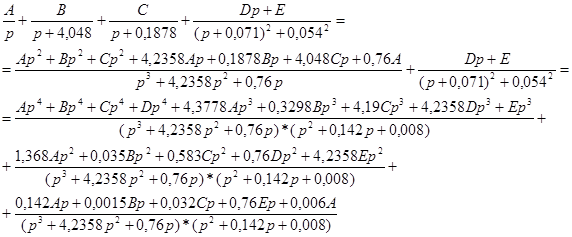
Составим систему уравнений и определим неизвестные коэффициенты А, В, С и D.

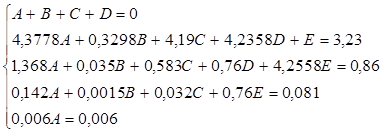
Решая полученную систему, получаем коэффициенты:

А = 1, В = -0,8108, С = 0,0029, D = -0,192, Е = -0,0788

Заменяя буквенные значения коэффициентов численными, и производя обратное преобразование Лапласа, получим:

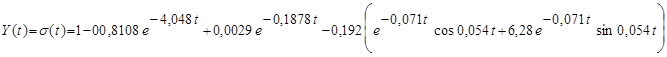
Подставим различные значения t в полученное уравнение и получим переходную характеристику. Для этого снова воспользуемся пакетом MSExcel. График будет иметь вид:

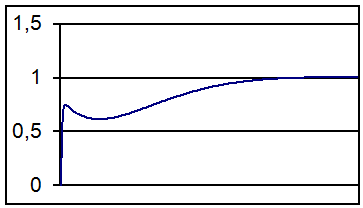
Как показали исследования, график переходной функции построенный в пакете VisSim30 аналогичен приведенному выше. Можно сделать вывод, что полученная переходная функция найдена верно.

Для нахождения основных показателей качества регулирования (ПКР), воспользуемся графиком, полученным при помощи пакета VisSim30.

Основными ПКР являются:

· Время переходного процесса t _п/п

· Вид переходного процесса (апериодический, колебательный, монотонный )

· Абсолютное перерегулирование s _абс

· Статическая ошибка e _ст