Курсовая работа: "Дискретні та неперервні динамічні системи в економіці" в MAPLE 7
(2.3.0)
та дослідити їх стійкість в лінійному наближенні.
Рішення:
1. Положення рівноваги вихідної динамічної системи (стаціонарні точки динамічної системи) визначається наступними умовами:
(2.3.1)
звідкіля маємо систему рівнянь рівноваги
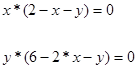(2.3.2)
Рішення системи рівнянь рівноваги (2.3.2) в пакеті MAPLE7 дає наступні 4 пари коренів – стаціонарних точок рівноваги динамічної системи (2.3.0):
> eqp1:=-x*x+2*x-x*y=0;
> eqp2:=-y*y+6*y‑2*x*y=0;
>
> solve({eqp1, eqp2}, {x, y});
(2.3.3)
2. Для дослідження стійкості кожного з отриманих рішень, складаємо системи першого наближення в околицях точок рівноваги за допомогою розкладення в ряд Тейлора. Формула Тейлора для функції двох змінних x, y у першому наближенні (тільки рівень 1 похідних) для функції 
в околицях точки x0 , y0 має наступний вигляд [7]:
(2.3.4)
Побудову систем рівнянь першого наближення системи (2.3.2) виконуємо за допомогою пакета MAPLE7 [4]:
> DxDt:=-x*x+2*x-x*y;
> mtaylor (DxDt, [x=0, y=0], 2);
> mtaylor (DxDt, [x=2, y=0], 2);
> mtaylor (DxDt, [x=4, y=-2], 2);
> mtaylor (DxDt, [x=0, y=6], 2);
(2.3.5)
> DyDt:=-y*y+6*y‑2*x*y;