d₂ = mz₂ = 8×60 = 480 мм

Уточняем межосевое расстояние

Определяем ширину колес

[b] = a_w · ψ_ba = 320 · 0,42 = 134,4 мм

Принимаем b = 130 мм.

Назначаем седьмую степень точности передачи [2, с. 32].

При модуле m = 8 мм и ширине венца b = 130 мм определяем контактные напряжения на активных поверхностях зубьев

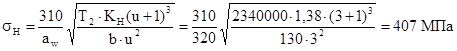
где К_Н – уточненный коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба

К_Н = К_{Н b} × К_{Н u} = 1,25 × 1,1 = 1,38

К_{Н b} = 1,25 [2, с. 32] – при несимметричном расположении колес относительно опор валов;

К_{Н u} = 1,1 [2, с. 40] – при окружной скорости передачи u£ 1 м/с и коэффициенте ширины венца y_ba = 0,42.

Из расчета видно, что контактные напряжения на активных поверхностях зубьев не превышает предельно допустимых для выбранного материала и термообработки

s_Н = 407 МПа < [s_Н ] = 409 МПа

Следовательно, колеса удовлетворяют требованиям контактной выносливости.

Определяем окружную силу, действующую в зацеплении

Определяем радиальную силу, действующую в зацеплении

F_r = F_t × tga = 9975 × tg20° = 3631 Н

где a = 20° - угол зацепления.

Проверяем зубчатые зацепления на изгибную прочность.

Определяем допускаемые напряжения изгиба

где – предел усталостной прочности при изгибе для стали 45 нормализованной при отнулевом цикле изменения напряжений изгиба

= 1,8 · HВ = 1,8 · 210 = 378 МПа

[S_F ]’ = 1,75 [2, с. 44] – коэффициент безопасности;

[S_F ]” = 1 [2, с. 45] – коэффициент, учитывающий непостоянство механических свойств материала и зависящий от метода получения заготовки (для штампованных заготовок).

При работе цилиндрической прямозубой передачи при одинаковых материалах и ширинах зубчатых венцов наибольшие изгибные напряжения возникают у зубчатых колес имеющих меньшее число зубьев, поэтому проверочный расчет на прочность при изгибе будем проводить для колеса z₁ .

Определяем действующие изгибные напряжения для колеса z₁ .