Курсовая работа: Расчет двухступенчатого редуктора

,

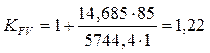K_f =1 · 1,22 · 1,0923· 1 = 1,333

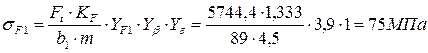
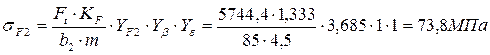
2.1.4 Проектировочный расчет на сопротивление усталости зубьев при изгибе

Определяют допускаемое напряжение изгиба, не вызывающее усталостной поломки зуба, МПа

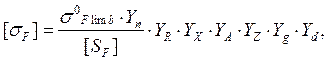
где: σ⁰ _Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа:

σ⁰ _Flimb1 = 1,75Н_НВ = 1,75 ·285 = 498,75;

σ⁰ _Flimb2 = 1,75Н_НВ = 1,75 ·248 = 367,04;

[S_F ] – минимальный коэффициент запаса прочности:

[S_F ] = 1,7;

Y_R – коэффициент, учитывающий шероховатость переходной поверхности

Y_R = 1 для неполированных поверхностей;

Y_Х – коэффициент, учитывающий размеры зубчатого колеса

Y_Х1 = 1.05 - 0.000125 ∙ d = 1,05 - 0.000125 ∙ 112,5 = 1,036

Y_Х2 = 1.05 - 0.000125 ∙ d = 1,05 - 0.000125 ∙ 193,5 = 1,026

Y_А – коэффициент, учитывающий влияния двухстороннего приложения нагрузки :

Y_А = 1 при одностороннем приложении;

Y_Z – коэффициент, учитывающий способ получения заготовки зубчатого колеса:

Y_Z = 1 для поковок и штамповок;

Y_g – коэффициент, учитывающий влияния шлифования переходной поверхности зуба:

Y_g = 1 при улучшении – если переходная поверхность зубьев не шлифуется;

Y_d – коэффициент, учитывающий влияние деформационного упрочнения или электрохимической обработки переходной поверхности:

Y_d = 1 – если переходная поверхность зубьев не подвергается деформационному упрочнению или электрохимической обработке;

Y_N – коэффициент долговечности:

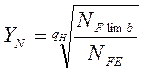, причём 1 ≤ Y_N ≤ Y_Nmax

где: N_Flimb – базовое число циклов напряжений; N_Hlimb = 4 ∙ 10⁶ ;

q_F – показатель степени кривой усталости при расчёте на сопротивление усталости при изгибе (для стальных колес с нешлифованной переходной поверхностью: