Курсовая работа: Расчет двухступенчатого редуктора

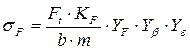, где

b - ширина венца зубчатого колеса, мм. В цилиндрических передачах:

b₂ = b_{w =} 85 мм, b₁ = b_w + (3...4) = 45 + 4 = 89 мм;

Y_F - коэффициент, учитывающий форму зуба и концентрацию напряжений. Определяют по таблице 2.8 /8/: для косозубых и шевронных цилиндрических колес - по числу зубьев эквивалентного колеса Z_v = Z/cos³ β:

Y_F = 3,9 при Z₁ = 25 и Х₁ = 0;

Y_F = 3,65 + (50 - 43)·0,05/10 = 3,685 при Z₂ = 43 и Х₁ = 0;

Y_β - коэффициент, учитывающий влияние наклона зуба:

Y_β =l - ε_β · β / 120⁰ >0,7, Y_β =l;

Y_ε - коэффициент, учитывающий влияние перекрытия зубьев:

Y_ε = 1 для прямозубых передач. Для косозубых:

Y_ε = 0,2 + 0,8/ε_α при ε_β < 1;

Y_ε = 1/ ε_α при ε_β ≥ 1;

K_F - коэффициент нагрузки при расчете на изгиб :

Kf =К_а ·K_fv ·K_Fβ ·К_Fα ,

где K_FV – коэффициент, учитывающий внутреннюю динамическую нагрузку, возникающую в зацеплении при расчете на изгиб:

К_Fβ - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий. Определяют по таблице 2.3 - для цилиндрической передачи /8/:

Ψ_bd = 0,7225 К_Fβ = 1,1 – (0,8 – 0,7225)·0,02/0,2 = 1,0923;

K_Fa - коэффициент, учитывающий распределение нагрузки между зубьями:

K_Fa = 1 для прямозубых передач.

K_Fa= =1,35 для косозубых передач;

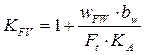, где

W_FV - удельная окружная динамическая сила при расчете на изгиб, Н/мм:

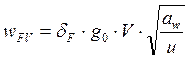,где

δ_F - коэффициент, учитывающий влияние вида зубчатой передачи:

δ_F =0,16-для прямозубых передач;

δ_F =0,06-для косозубых и шевронных./8/:

g_o - коэффициент, учитывающий влияние разности шагов зубьев шестерни и колеса, определяют по таблице 2.6 /8/:

g_o = 5,6 для 8 степени точности и модуле < 3,55;

g_o = 6,1 для 8 степени точности и модуле 3,55…10;