Курсовая работа: Расчёт и анализ надёжности системы восстанавливаемых объектов

В данной курсовой работе произведён расчёт и анализ надежности технической системы без учета нагрузки.

Курсовая работа содержит:

формул 2,

таблиц 4,

рисунков 4.

Введение

Системы электроснабжения относятся к классу сложных технических систем и определяются множеством свойств, из которых к числу важнейших относится свойство надежности технической системы.

Надежная работа устройств системы электроснабжения является необходимым условием обеспечения качественной и устойчивой работы железнодорожного транспорта. Анализ и обеспечение работоспособного состояния систем электроснабжения на этапах проектирования и эксплуатации – сложная задача, для решения которой используется математический аппарат теории надежности.

Задание на расчёт

· Определить оценки показателей надежности (коэффициент готовности) для элементов системы, показанной на схеме замещения, по данным статистки отказов и восстановления за период эксплуатации N лет, с учетом паспортных данных.

· Составить модель структуры сети для анализа надежности логико-вероятностным методом и определить значения ее показателей. Рассчитать и построить графики зависимости коэффициента готовности системы и вероятности отказа питания от каждого источника генерации на L последующих лет эксплуатации, с разбивкой по кварталам.

· Сделать выводы о необходимости технического обслуживания по критерию минимально допустимого уровня надежности.

Условия расчета : пренебречь ненадежностью источников питания и шин 110 и 10 кв. Законы распределения отказов и восстановления принять экспоненциальными, отказы элементов - независимыми. Для двухцепных ЛЭП учитывать только отказ 2-х цепей. Для трансформаторов учитывать только восстановление аварийным ремонтом.

Принять в данной задаче, что пропускная способность всех устройств сети выше максимальной нагрузки.

ИСХОДНЫЕ ДАННЫЕ

Схема замещения заданной подстанции показана на рис 1, ее описание и исходные данные приведены в табл. 1.

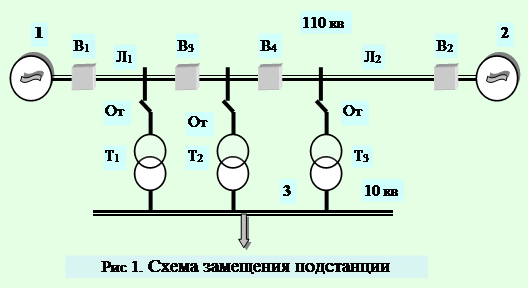Описание схемы и параметры расчета:

· Длина линий: Л₁ = 42 км; Л₂ = 142 км. Линия Л₂ – двухцепная.

· Выключатели: В₁ и В₂ - масляные, В₃ – воздушный.

· Период эксплуатации N = 6 лет; период прогнозирования L = 3 года.

· Минимально допустимый уровень надежности k_Гдоп = 0.89 .

Все выключатели и отделители включены.

Таблица 1

Исходные данные по элементам схемы

Элемент	λ – частота отказов, откл/год		t в - ср. время восстановления, 10-3 лет/отказ		Число отказов		Время восстановления 10-3 лет/отказ
	Паспортные данные				Статистика отказов
В1	0.01		2.5		2		26.8; 12.6
В2	0.01		2.5		3		31.5; 17.6; 23.7
В3	0.07		2.5		0		-
В4	0.01		2.5		2		18.6; 42.2
Л1	0.592		0.5		1		16.4
Л2	0.625		3.0		0		-
От1	0.013		0.4		0		-
От2	0.013		0.4		0		-
От3	0.013		0.4		0		-
Т1	0.01		60.0		0		-
Т2	0.01		60.0		0		-
Т3	0.01	60.0		0		-

Решение

Жирным шрифтом (табл. 1) выделены параметры линий, пересчитанные на их конкретную длину:

Л1 :	1.41·(42 км/100 км) = 0.592 откл/год;
Л2 :	0.44·(142 км/100 км) = 0.625 откл/год.

По данным статистики отказов, рассчитаем оценки частоты отказов и среднего времени их восстановления.

g = N /M ; λ i * = (1-g) · λ i + g ·(ni \N); t в i * = (1-g) · t в i + g · ( );

(1)

где N - период эксплуатации; M= N+15 – полное «время старения» априорных данных; i – номер элемента, n_i – число отказов i-го элемента за период эксплуатации; j - индекс; - время восстановления i-го элемента при j -м отказе. Верхним индексом * отмечены оценки параметров – эти значения должны быть использованы в формуле коэффициентов готовности элементов.

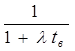k_г =. (2)

Приведем пример расчета для одного из отказавших элементов (выключатель В₁ ):

· вес измерений определим как «коэффициент старения информации»:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--