Курсовая работа: Расчёт и анализ нерекурсивного цифрового фильтра

Точность аппроксимации оценивалась по формуле (32). В таблице (5) приведены результаты расчёта

Результаты расчета точности аппроксимации для метода наименьших квадратов

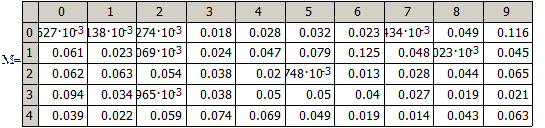
В таблице 6 приведена максимальная (абсолютная) погрешность аппроксимации для различных значений N.

Абсолютная погрешность аппроксимации для метода наименьших квадратов

Абсолютная погрешность аппроксимации АЧХ
N=135	N=25	N=32
0,125	0,057	0,051

2.3 Сравнение методов расчёта

Сравнивая результаты расчётов точности аппроксимации, приведённые в таблицах 2 и 6, можно сделать вывод, что метод наименьших квадратов обеспечивает более точную аппроксимацию при N=25 амплитудно-частотной характеристики по сравнению с методом частотной выборки. С увеличением порядка фильтра N точность аппроксимации увеличивается для обоих методов, но точность метода наименьших квадратов начинает уменьшаться по сравнению с методом частотной выборки.

Заключение

В данной курсовой работе был рассмотрен расчёт нерекурсивного цифрового фильтра двумя методами: методом наименьших квадратов и методом частотной выборки. Результаты расчётов точности аппроксимации для каждого метода позволяют сделать следующие выводы:

· Точность аппроксимации увеличивается с увеличением N (порядка фильтра)

· Метод наименьших квадратов обеспечивает более точную аппроксимацию при средних значениях N.