Курсовая работа: Расчет напряженно-деформированного состояния конечно-элементной модели металлоконструкции пролетной

Предельное расстояние между поперечными основными ребрами жесткости «а» не должно в стальных конструкциях превышать:

при λ₀ > 3,2 – тогда шаг а ≤ 2h₀ ;

при λ₀ ≤ 3,2 – тогда шаг а ≤ 2,5h₀ .

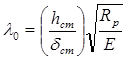, (8)

где h_ст – высота стенки;

R_p – расчетное сопротивление материала стенки, согласно таблицы 1.5.11 [1],

R_p =240 МПа;

E – модуль упругости материала стенки, E = 210000 МПа.

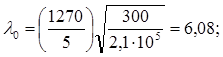следовательно, шаг равен: а ≤ 2h₀ ;

Поперечные ребра следует устанавливать также в местах приложения к верхнему поясу больших неподвижных сосредоточенных грузов.

В главной балке имеется три характерных отсека, на которые она делится основными вертикальными ребрами жесткости (диафрагмами).

Отсек на опоре отличается тем, что в нем действуют максимальные касательные напряжения от поперечной силы, а нормальные напряжения равны нулю, так как на опоре изгибающий момент равен нулю.

Отсек в середине пролета отличается тем, что в нем действуют максимальные нормальные напряжения, а касательные напряжения равны нулю.

И отсек в средней четверти пролета, который отличается тем, что в нем действуют одновременно и касательные и нормальные напряжения, хотя и те и другие не принимают максимальных значений.

Для отсека на опоре критические напряжения определяются по формуле:

(9)

где “а” и “b” – большая и меньшая стороны прямоугольника (отсека) соответственно, b = h₀ ;

δ – толщина стенки.

Условие обеспечения местной устойчивости при расчете по методу предельных состояний:

, (10)

где τ - напряжение определяется с учетом коэффициентов перегрузки.

В среднем отсеке критическое напряжение определяется по формуле:

(11)

В том отсеке, где действуют и касательные и нормальные напряжения, для обеспечения устойчивости должно выполняться условие:

(12)

Кроме вертикальных ребер жесткости для обеспечения местной устойчивости стенок могут потребоваться продольные ребра жесткости.

Если

, (13)

то продольные ребра не требуются.