Курсовая работа: Расчет параметров вентильного электропривода

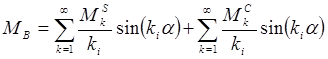(27)

где

и - амплитуды синусной и косинусной составляющих в ряду Фурье.

k_i - номер гармоник разложения.

Суммарный момент выглядит следующим образом:

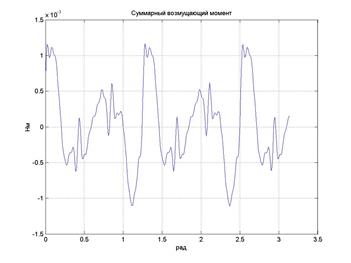
Рис 10. Суммарный момент возмущения.

Время динамического запаздывания (сек) из ФЧХ по току и угловой скорости для управления:

Частота (Гц)	0,1592	1,1273	2,0955	3,0637	4,0318	5,0000
Время запаздывания по току	3,1312	0,4331	0,2283	0,1530	0,1139	0,0901
Время запаздывания по скорости	0,0104	0,0104	0,0103	0,0102	0,0101	0,0099

Заключение

В курсовой работе была проанализирована математическая модель вентильного электропривода, построены частотные графики модели (по току и по W), а так же графики переходных процессов при различных программных напряжениях. На основании вида этих графиков, а также проведенного расчета устойчивости можно сделать вывод о устойчивости вентильного электропривода (его математической модели).