Курсовая работа: Расчет показателей надежности и законов их распределения
Таблица 4 - Выравнивание статистического ряда по экспоненциальному закону
| W | f | W-X | x=Wi/X | ℓ | (Nk/X)*ℓ | f' |
| 16,09 | 0,00 | 10,76 | 3,02 | 0,026 | 0,488 | 0,00 |
| 14,09 | 0,00 | 8,76 | 2,64 | 0,035 | 0,657 | 1,00 |
| 12,09 | 0,00 | 6,76 | 2,27 | 0,492 | 0,657 | 1,00 |
| 10,09 | 2,00 | 4,76 | 1,89 | 0,077 | 1,435 | 1,00 |
| 8,09 | 9,00 | 2,76 | 1,52 | 0,135 | 2,538 | 3,00 |
| 6,09 | 16,00 | 0,76 | 1,14 | 0,237 | 4,445 | 4,00 |
| 4,09 | 14,00 | -1,24 | 0,77 | 0,415 | 7,782 | 8,00 |
| 2,09 | 9,00 | -3,24 | 0,39 | 0,733 | 13,760 | 14,00 |
| Всего | 50,00 | 31,76 | 32,00 |
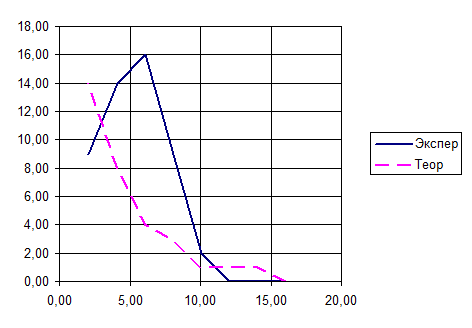
Рисунок 1 - Выравнивание статистического ряда по экспоненциальному закону распределения
3.1.1 Оценка различий эмпирического и теоретического распределений
Методика оценки различий эмпирического и теоретического распределений для различных законов распределения одна и та же.
Для проверки согласованности теоретического и эмпирического распределений чаще всего используют критерий c2 Пирсона, величину которого рассчитывают по формуле
где c02 – стандартные значения критерия, его значения находят по специальным таблицам в зависимости от числа степеней свободы v;
, 
– эмпирические и теоретические частоты классов соответственно.
Первичное v1 и вторичное v2 числа степеней свободы определяют по следующим формулам:
; 
; 
.
где r1,r2 - числа классов до и после объединения классов с малыми теоретическими частотами.
Крайние классы с частотой 
<
объединяют с соседними классами ( – минимально допустимая теоретическая частота крайних классов в зависимости от начального числа степеней свободы)
Различия распределений могут считаться случайными, если эмпирический критерий не достигает требуемого порога вероятности b. Необходимо ориентироваться на три уровня вероятности: при малой ответственности исследований b1>= 0,999; при обычной b2 >= 0,99; при большой b3 >= 0,95.
Таблица 5 - Определение различий законов распределения
| W1 | f | f ' | f-f ' | (f-f ' )^2 | ( f-f ' )^2/f ' |
| 16,1 | 0 | 0,49 | -0,49 | 0,24 | 0,49 |
| 14,1 | 0 | 0,66 | -0,66 | 0,43 | 0,66 |
| 12,1 | 0 | 0,66 | -0,66 | 0,43 | 0,66 |
| 10,1 | 2 | 1,44 | 0,56 | 0,32 | 0,22 |
| 8,1 | 9 | 2,54 | 6,46 | 41,75 | 16,45 |
| 6,1 | 16 | 4,44 | 11,56 | 133,53 | 30,04 |
| 4,1 | 14 | 7,78 | 6,22 | 38,66 | 4,97 |
| 2,1 | 9 | 13,76 | -4,76 | 22,66 | 1,65 |
| Всего | 50 | 31,762 | 55,13 |
Следовательно, c02: 13,3; 18,5 при b соответственно, 0,99, 0,999
Таким образом, при b=0,99 и 0,999 ответственности испытаний c2 больше c02, то есть эмпирическое распределение противоречит экспоненциальному закону распределения.
3.2 Нормальный закон распределения
Таблица 6 - Выравнивание статистического ряда по нормальному закону
| Нормальный закон | ||||||
| Теор частоты | ||||||
| W | f | W-X | x=(W-Ч)/сигма | f(x) | Nkf(x)/сигма | f' |
| 16,09 | 0,00 | 10,76 | 4,87 | 0,00 | 0,000 | 0,00 |
| 14,09 | 0,00 | 8,76 | 3,97 | 0,00 | 0,007 | 0,00 |
| 12,09 | 0,00 | 6,76 | 3,06 | 0,00 | 0,167 | 0,00 |
| 10,09 | 2,00 | 4,76 | 2,15 | 0,04 | 1,773 | 2,00 |
| 8,09 | 9,00 | 2,76 | 1,25 | 0,18 | 8,277 | 8,00 |
| 6,09 | 16,00 | 0,76 | 0,34 | 0,38 | 17,026 | 17,00 |
| 4,09 | 14,00 | -1,24 | -0,56 | 0,34 | 15,431 | 15,00 |
| 2,09 | 9,00 | -3,24 | -1,47 | 0,14 | 6,162 | 6,00 |
| Всего | 50,00 | 48,84 | 48,00 | |||
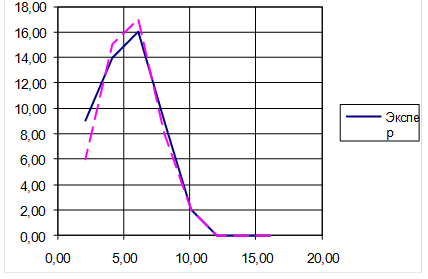
Рисунок 2 - Выравнивание статистического ряда по нормальному закону распределения
Таблица 7 - Определение различий законов распределения
| W1 | f | f ' | f-f ' | (f-f ' )^2 | ( f-f ' )^2/f ' |
| 16,1 | 0 | 0,00 | 0,00 | 0,00 | 0,00 |
| 14,1 | 0 | 0,01 | -0,01 | 0,00 | 0,01 |
| 12,1 | 0 | 0,17 | -0,17 | 0,03 | 0,17 |
| 10,1 | 2 | 1,77 | 0,23 | 0,05 | 0,03 |
| 8,1 | 9 | 8,28 | 0,72 | 0,52 | 0,06 |
| 6,1 | 16 | 17,03 | -1,03 | 1,05 | 0,06 |
| 4,1 | 14 | 15,43 | -1,43 | 2,05 | 0,13 |
| 2,1 | 9 | 6,16 | 2,84 | 8,06 | 1,31 |
| Всего | 50 | 48,842 | 1,77 |
Следовательно, c02:11,1; 15,1; 20,5 при b соответственно 0,95, 0,99, 0,999
Таким образом, при b=0,99 и 0,999 ответственности испытаний c2 меньше c02, то есть эмпирическое распределение не противоречит нормальному закону распределения.
3.3 Распределение Вейбула
Таблица 8 - Выравнивание статистического ряда по распределение Вейбула
| W | f | Wi /a | x=af (Wi/a) |
| f' |
| 16,09 | 0,00 | 2,74 | 1,2134 | 20,636 | 20,6 |
| 14,09 | 0,00 | 2,40 | 1,4715 | 25,026 | 25,0 |
| 12,09 | 0,00 | 2,06 | 1,5130 | 25,731 | 25,7 |
| 10,09 | 2,00 | 1,72 | 1,3597 | 23,124 | 23,1 |
| 8,09 | 9,00 | 1,38 | 1,0791 | 18,352 | 18,4 |
| 6,09 | 16,00 | 1,04 | 0,7590 | 12,908 | 12,9 |
| 4,09 | 14,00 | 0,70 | 0,4697 | 7,988 | 8,0 |
| 2,09 | 9,00 | 0,36 | 0,2495 | 4,243 | 4,2 |
| Всего | 50,00 | 138,01 | 137,90 |
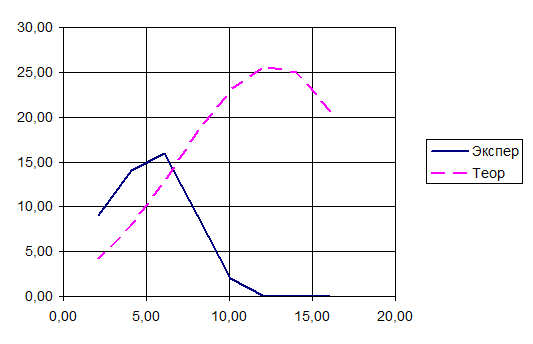
Рисунок 3 - Выравнивание статистического ряда по распределению Вейбула