Курсовая работа: Расчет симметричных автоколебаний нелинейной САР

Бывают случаи, когда автоколебания являются полезным явлением. Но также бывают и обратные, когда автоколебания желательно исключить. Наличие или отсутствие автоколебаний можно регулировать несколькими способами. Например, с помощью параметров самой системы (коэффициентов передачи), что и делается в данной работе, либо с помощью применения корректирующих цепей. Корректирующие цепи позволяют резко понизить амплитуду автоколебаний и поднять частоту или вовсе подавить их при малой зоне нечувствительности релейной характеристики.

1. Расчет

В начале расчета необходимо преобразовать исходную структурную схему с учетом задания. После преобразования получим расчетную схему (рис. 3), которая будет содержать последовательно соединенные линейную часть (ЛЧ) и нелинейный элемент (НЭ). Линейная часть представляет собой преобразованные в единый блок линейные элементы. Определим К_гр и ω_π при τ_гр =0, затем из условия единственности решения найдем τ_max =2π/ ω_π .

Рис. 3.

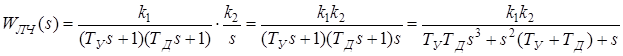
Примем k1k2= К

Минимальное значение коэффициента усиления К линейной части САУ, при котором автоколебания находятся на границе своего возникновения и исчезновения (полуустойчивы), называется граничным коэффициентом К_гр .

Для нахождения частоты w и Кгр запишем уравнение гармонического баланса

(1.1)

и, выделим в нем слева от знака равенства вещественную X(A,w) и мнимую Y(A,w) части:

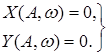(1.2)

В уравнении (1.1) приняты следующие обозначения: W_ЛЧ (jw) – частотная передаточная функция ЛЧ системы; W_НЭ (A) – комплексный коэффициент передачи гармонически линеаризованного нелинейного элемента (НЭ). Wнэ(А) = q(A).

Граничное значение коэффициента усиления Кгр можно определить из системы уравнений (1.2) при значении амплитуды А, соответствующей наименьшему значению модуля функции Z_НЭ (A) = -1/ W_НЭ (A). Построим график функции Z_НЭ (A) и найдем амплитуду А, используя программу Mathcad 2001.

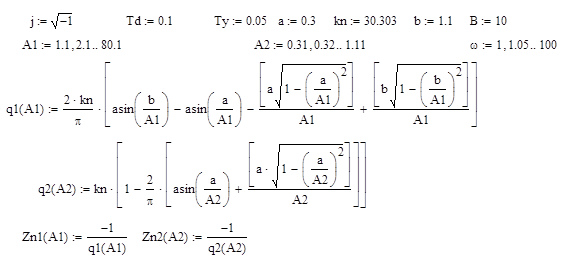
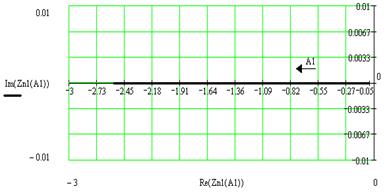
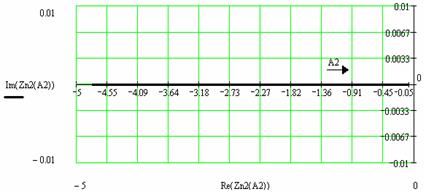
Рис. 4. Графики зависимости Z2_НЭ (A2) при a≤А2≤b и Z1_НЭ (A1) при А1≥b

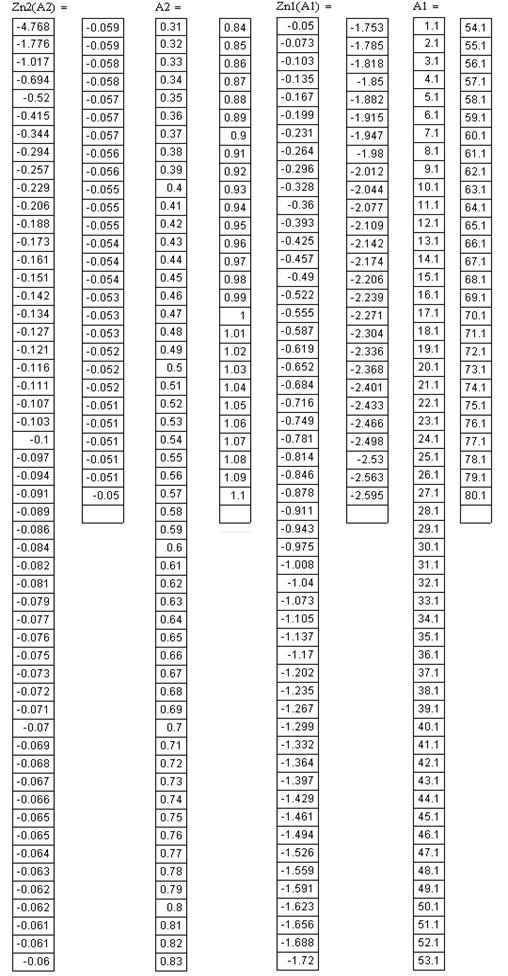
Исследуя вышеприведенные графики и значения, полученные в результате расчета Z2_НЭ и Z1_НЭ ,зависящих от A2 и A1 соответственно (Таблица 1.) приходим к выводу, что наименьшему значению модуля функции Z_НЭ (A) = -1/ W_НЭ (A) соответствует амплитуда A=b=1.1

Найдем значение Wнэ(А) = q(A) при А=1.1:

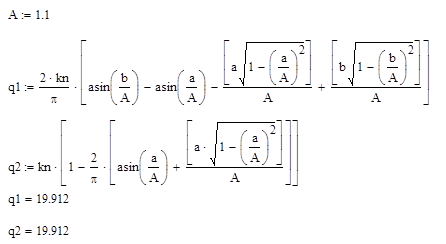
Теперь из системы уравнений (1.2) найдем граничное значение коэффициента усиления Кгр и частоту ω_π

Начальные условия:

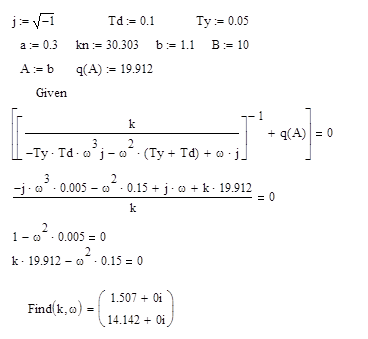
Согласно выше приведенным расчетам Кгр = 1.507, в соответствии с условием, что , в дальнейшем будем рассматривать К вместо произведения k1k2 и брать равным 1.45.

Найдем τ_max (с)

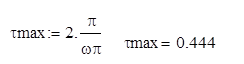
Значит, необходимое нам время запаздывания будет варьировать в следующих приделах 0≤τ≤ 0.444.

Таблица 1. Значения Z2_НЭ и Z1_НЭ ,зависящие от A2 и A1 соответственно при a≤А2≤b и А1≥b.

2. Расчёт амплитуды и частоты периодических режимов графоаналитическим методом гармонического баланса

Расчётная структурная схема состоит из последовательно соединённой, преобразованной в единый блок, линейной части ЛЧ и нелинейного элемента НЭ (рис.3.). При этом сигнал задания x_o полагается равный нулю, так как расчёт осуществляется для симметричных автоколебаний.

Условием возникновения периодических режимов в представленной на рис.3 нелинейной системе является основное уравнение гармонической линеаризации:

1+W_ЛЧ (jw)W_НЭ (A)=0, (2)

где W_ЛЧ (jw) - частотная передаточная функция ЛЧ;