Курсовая работа: Расчет технологических, теплотехнических и конструктивных параметров машин непрерывного литья заготовок

(3.2)

(3.3)

Безразмерное расстояние от уровня стали в кристаллизаторе

, (3.4)

где х - реальное расстояние, м;

- время нахождения заготовки на глубине х в кристаллизаторе, с; v - скорость заливки, м*с^-1 ; - коэффициент теплоотдачи от поверхности заготовки к охлаждающей воде, Вт*м^-2 *K^-1 :

(3.5)

где d - толщина зазора между заготовкой и стенкой кристаллизатора; - коэффициент теплопроводности жидкого вещества в зазоре; - толщина медной стенки кристаллизатора; - коэффициент теплопроводности меди; - коэффициент теплоотдачи от внешней стороны медной стенки кристаллизатора к охлаждающей воде (определяют по критериальным соотношениям).

Хилс использовал уравнение Nu = 0,023 (Re)^0,8 (Pr)^0,33 и параметры: Y- эффективная длина кристаллизатора, м (соответствует уровню стали в кристаллизаторе); - безразмерная длина кристаллизатора; - безразмерная толщина застывшей стали; - реальная толщина застывшей корки, м; - безразмерная температура поверхности заготовки; - реальная температура поверхности заготовки, °С; -температура солидуса; Н' = L₁ /(ct_S ) - безразмерное общее тепло затвердевания; L₁ - реальная скрытая теплота затвердевания (включая теплоту перегрева) (здесь t₁ - температура разливаемой стали); - безразмерное тепло, отведенное от части заготовки длиной х, приходящееся на единицу окружности кристаллизатора; - реальное тепло, отведенное из части заготовки длиной х, приходящееся на единицу окружности кристаллизатора за единицу времени.

Для расчета температуры застывшей корки в кристаллизаторе К. Фекете [6] разработал примерные упрощенные методы.

Он исходит из рассуждений, что кристаллизатор в МНЛЗ является теплообменником, работающим противоточно, так что можно считать, что разливаемая сталь охлаждается проточной водой. Им получено соотношение:

, (3.6)

где -разность температур между жидкой сталью и охлаждающей кристалли-затор водой; -разность температур обоих веществ при входе в кристаллиза-тор; -коэффициент теплоотдачи, Вт* м^-2 *К^-1 ; -охлаждающая внутренняя поверхность кристаллизатора, м² ; - энтальпия стали; - энтальпия воды, равная ; -внутреннее сечение кристаллизатора, м; v-скорость вытягивания, м*с ^-1 ; - плотность застывшей стали, кг*м ^-3 ; с - теплоемкость ста-ли, Дж * кг ^–1 * К^-1 .

На основании известных результатов изучения отвода тепла, проведен-ного X. Крайнером и Б. Тарманном [7], а также И. Саважем и В.Х. Притчардом [2], К. Фекете составил уравнение для отвода тепла кристаллизатором:

. (3.7)

Для определения средней плотности теплового потока от кристаллиза-тора на данном расстоянии х от уровня стали в кристаллизаторе необходимо проинтегрировать предыдущее соотношение:

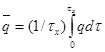; (3.8)

, (3.9)

где - время, с.

При описании передачи тепла от твердого тела к обтекающей его жидко-сти или газу имеется в виду теплообмен. Количество тепла Q, Дж, переходящее с поверхности тела в окружающую среду, определяют по формуле Ньютона:

(3.10)

где - коэффициент теплоотдачи, Вт м^-2 К^-1 ; t_п – температура поверхности тела, ⁰ С; t_ср – температура окружающей среды, ⁰ С; S – охлаждаемая площадь, м² ; - время, с.

Согласно уравнению Ньютона получим:

(3.11)

где , К - среднелогарифмическая разность температур в кристаллиза-торе между сталью и охлаждающей водой:

(3.12)

Здесь (индекс 1 относится к стали, 2 - к воде; р - для температуры входа; к - выхода).

Из теории расчета теплового обмена известно, что среднелогарифмическую разность можно заменить среднеарифметической, если