Курсовая работа: Расчет установившегося режима работы электрической системы
Матрица Якоби не должна быть вырожденной, тогда решая полученную систему (линейную) любым способом, находим первое приближение переменных:
![]()
Каждый шаг итерационного процесса состоит из решения линейной системы:
![]()
и определения следующего приближения неизвестных:
![]()
Контроль сходимости осуществляется по вектору невязок:
![]()
Уравнение узловых напряжений в форме баланса мощностей для ![]() -го узла можно записать в следующем виде:
-го узла можно записать в следующем виде:
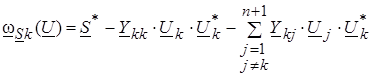
Слагаемое ![]() внесено в сумму, балансирующему узлу присвоен номер
внесено в сумму, балансирующему узлу присвоен номер ![]() .
.
Выделим в уравнении действительные и мнимые части:
![]()
где ![]() ,
, ![]() – соответственно небалансы активных и реактивных мощностей в узле
– соответственно небалансы активных и реактивных мощностей в узле ![]() ;
;
![]() ,
, ![]() – вектор-столбцы действительных и мнимых составляющих напряжений.
– вектор-столбцы действительных и мнимых составляющих напряжений.
В расчетах на ЭВМ обычно в качестве неизвестных используются модули и фазы напряжений узлов ![]() и
и ![]() .
.
Уравнение баланса мощностей для ![]() -го узла при переменных
-го узла при переменных ![]() и
и ![]() :
:
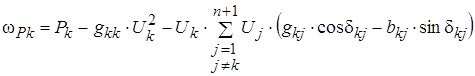
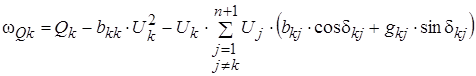
где ![]()
Уравнение в форме баланса мощностей:
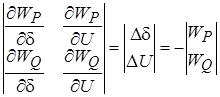
С учетом реальных условий в электрических системах можно пренебречь недиагональным элементами матрицы Якоби, т.е.
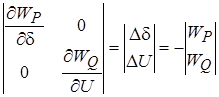
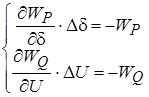
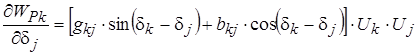
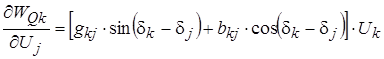
Метод Ньютона очень быстро сходится и имеет высокую надежность.
Результаты решения нелинейных уравнений узловых напряжений в форме баланса мощностей в полярной системе координат в среде MathCAD методом Ньютона, а так же сама программа расчета, приведены в Приложении.