Курсовая работа: Рассеяние волн в задаче о маскировке объектов методом волнового обтекания

Тогда дифференциал рассеянной мощности через площадку принимает следующий вид:

. (1.2.10)

Дифференциал телесного угла в сферических координатах r, θ_s , φ_s

Теперь, подставляя (1.2.7) в (1.2.10) получим следующее выражение для мощности, рассеянной в элемент телесного угла:

. (1.2.11)

Разделив левую и правую части выражения (1.2.11) на вектор Умова-Пойтинга для падающей волны (1.2.4), получим

. (1.2.12)

Размерность последнего соотношения является размерностью площади. называется дифференциальным сечением рассеяния и обозначается как .

А интегрирование 1.2.12, в свою очередь, даёт

. (1.2.13)

, (1.2.14)

где – рассеянная мощность, а – сечение рассеяния.

. (1.2.15)

1.2 Решение задачи о рассеянии на цилиндре

Решается задача о нахождении полей на таком удалении от точек рассеяния, что фронт распространения волн этих полей можно считать плоскостью. Найдём для этого сперва общее решение, характеризующее бесконечно длинный цилиндр, а затем подставим в решение граничные условия, обобщив его тем самым на цилиндр длинны L.

Пусть поле падающих волн задаётся выражением:

, (1.2.1)

где (см. рис. 2.1), падающая волна раскладывается в суперпозицию двух поляризаций – горизонтальной линейной и вертикальной линейной, а и горизонтальный и вертикальный вектора поляризации.

Падающая волна также может быть представлена в виде векторных цилиндрических волн, т.е. следующим образом:

. (1.2.2)

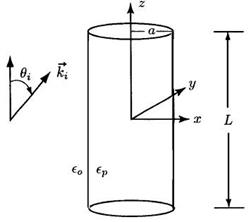
Цилиндр высоты L, радиуса a и проницаемости

Общее решение будет состоять из выражений для рассеянного поля и поля внутри цилиндра объединённых граничными условиями. Запишем теперь выражения, определяющие рассеянное и внутренне поля с точностью до неизвестных коэффициентов , , ,на оговоренном ранее расстоянии от точки рассеяния

, (1.2.3)

, (1.2.4)

где , – символ, с помощью которого обозначается конфигурация функций Бесселя и Ханкеля для величин, перед которыми он стоит, а – коэффициенты, получаемые с использованием преобразования Фурье от выражения (1.2.1)

,

известны для такого приближения.