Курсовая работа: Разработка системы для оценки перспективности производственных направлений на предприятии

КП - Производство компьютерной периферии

НБ - Производство ноутбуков

Для определения значений попарных сравнений воспользуеся соотношением (1.2).

, где (1.1.3)

- сравнение i-го и j-го вида продукции, d_j – спрос на j-й вид продукции.

Таким образом, таблица попарных сравнений будет иметь вид

РС	СР	СО	КП	НБ
РС	1	10	2,857	1,818	0,596
СР	0,017	1	0,114	0,122	0,027
СО	0,03	1,4	1	0,256	0,093
КП	0,089	2,142	0,624	1	0,147
НБ	0,219	6	1,688	1,091	1

Из таблицы видно, что Рабочие станции по сравнению с Серверами оценены как 10, соответственно Сервера по сравнению Рабочими станциями в 0,017.

Анализ приоритетов производится с использованием «Модуля формирования режима работы производства, на основе оценки приоритетов».

1.2 Метод Крылова

Метод Крылова основан на свойстве квадратной матрицы М обращать в нуль свой характеристический многочлен. В данной работе матрица М -это матрица коэффициентов технологических связей, которая имеет вид:

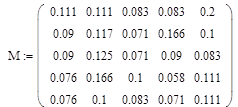
Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем своего характеристического многочлена и, следовательно, обращает его в нуль. Пусть (1.2.1) характеристический многочлен

(1.2.1)

Заменяя в выражении величину λ на M, получаем

(1.2.2)

Взяв произвольный ненулевой вектор У⁰ и умножив обе части выражения (1.2.2) на него, получим:

(1.2.3)

Положим

(1.2.4)

Тогда

(1.2.5)

Или в виде

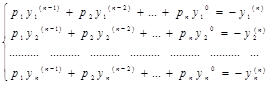
Если эта система имеет единственное решение, то ее корни р₁ , р₂ …..р_{n ,} являются коэффициентами характеристического многочлена (1.2.1).

Если известны коэффициенты р₁ , р₂ …..р_{n ,} и корни λ₁ , λ₂ ,….λ_n характеристического многочлена, то метод Крылова дает возможность найти соответствующие векторы по следующей формуле:

, (1.2.6)

Здесь y^{( n -1)} , y^{( n -2)} , …. y⁽⁰⁾ – векторы, использованные при нахождении коэффициентов р₁ , р₂ …..р_n методом Крылова, а коэффициенты q_ij () определяются по схеме Горнера

q_0i = 1, q_ij = λ_i q_i-1,i +p_i (1.2.7)

Для определения собственных чисел матрицы М необходимо решить полученное характеристическое уравнение. Для матрицы М это уравнение будет пятой степени, решать такое уравнение в данной работе будем решать, используя метод касательных или иначе метод Ньютона.