Курсовая работа: Реализация алгоритма обратной трассировки лучей для моделей с большим числом полигонов
коэффициента преломления
коэффициента поглощения
коэффициента отражения
Так как я не моделирую диффузное отражение и преломление, то не смогу получить фоновую подсветку. Поэтому вводим минимальную фоновую освещенность. Часто она позволяет просто значительно улучшить качество изображения.
Алгоритм трассировки позволяет рисовать очень качественные тени. Это не потребует большой переделки алгоритма. В него придется кое-что добавить. При расчете освещенности точки необходимо пустить в каждый из источников света "Теневой фронт". "Теневой фронт" - это луч, с помощью которого проверяется, лежит ли что-нибудь между точкой и источником. Если между ними лежит непрозрачный объект, то точка находится в тени. Это значит, что данный источник, не делает свой вклад в итоговую освещенность точки. Если лежит прозрачный объект, то интенсивность источника уменьшается. Прорисовка теней является очень затратной по времени. Так что, в некоторых ситуациях их отключают.
В моей программе есть возможность включить сглаживание изображения. Сглаживание заключается в том, что для определения цвета пиксела. пускается не один луч, а четыре и определяется среднее значение цвета у этих лучей. Если необходимо найти цвет пиксела (i,j), то пускаются 4 луча в точки экранной плоскости с координатами (i-0.25,j-0.25), (i-0.25,j+0.25), (i+0.25,j-0.25), (i+0.25,j+0.25).
2.3.2 Математическая основа обратной трассировки лучей
Координаты всех объектов сцены определены в некой глобальной системе координат (в том числе и камеры). После формирования первичного луча создадим подсистему, у которой центр совпадает с точкой выхода луча и ось OZ направлена по лучу. Вычислим матрицу перехода из первой системы координат во вторую. Это позволит просто искать пересечения с треугольником, со сферой, векторы преломления и отражения. При необходимости переводим координаты нужных объектов в новую систему координат и работаем уже в ней. Если необходимо построить вторичный луч, создаем еще одну систему координат, связанную с вторичным лучом, и считаем матрицу для перехода из 2 системы в 3. Чтобы получить матрицу перехода из 1 в 3 необходимо умножить матрицу перехода из 2 в 3 умножить на матрицу перехода из 1 в 2. Таким образом, мы работаем все время в какой-то подсистеме. Нам не надо переводить никакие координаты обратно в глобальную систему. Поэтому не надо и составлять обратную матрицу.
2.3.3 Составление матрицы
Составление матрицы преобразования из текущей системы координат в систему координат, центр которой находится в точке (x, y, z) и ось OZ которой направлена по (dx, dy, dz). Для такого преобразования необходимо:
совершить сдвиг в точку (x, y, z)
совершить поворот вокруг OZ
совершить поворот вокруг OX
1. Матрица сдвига: 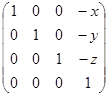 .
.
2. Необходимо совершить поворот вокруг оси OZ по часовой стрелке на угол α.
![]()
![]() .
.
Матрица поворота, таким образом, будет равна:
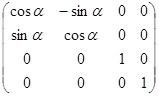
3. Необходимо совершить поворот вокруг оси OX по часовой стрелке на угол β.
![]()
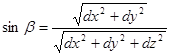 .
.
Матрица поворота, таким образом, будет равна:
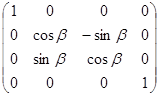
Умножив M3 на M2 , а результат на M1 получим искомую матрицу перехода:
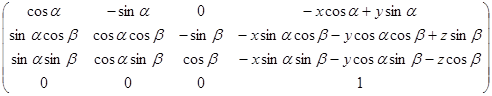
2.3.4 Программная реализация
Во многих функциях и процедурах в программе в качестве входных и выходных параметров выступают матрицы. Поэтому в программе введен специальный тип:
TMatrix=Array [0. .11] of real
Это массив из 12 элементов типа real. Он представляет собой последовательно записанные три верхние строчки матрицы. Я не включил последнюю строчку, так как она одинаковая у всех матриц преобразования и равна (0, 0, 0,1).
Для операций над матрицами в программе предусмотрены следующие процедуры:
1. Procedure MatrixAB (var Res: TMatrix; const M1,M2: TMatrix)
Процедура умножает матрицу M1 на матрицу M2 и помещает результат в Res.
2. Procedure ShiftMatrix (var M: TMatrix; Z: real)