Курсовая работа: Реализация алгоритма обратной трассировки лучей для моделей с большим числом полигонов

Процедура перемещает систему координат, задаваемую матрицей M, по оси OZ на z.

3. Procedure SetMatrix (var M: TMatrix; dx,dy,dz,x,y,z: real) overload

Создает матрицу перехода из текущей системы координат в систему координат, находящуюся в точке (x,y,z), ось OZ которой направлена по вектору (dx,dy,dz).

4. Procedure SetMatrix (var M: TMatrix; dx,dy,dz: real) overload

Создает матрицу перехода из текущей системы координат в систему координат, ось OZ которой направлена по вектору (dx,dy,dz).

Преобразование координат

Для преобразования координат точки из одной системы координат в другую необходимо умножить матрицу преобразования на столбец координат точки.

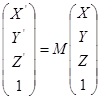
Для преобразования точки из одной системы координат в другую в программе существует процедура Trans (const M: TMatrix; var F: TPoint; const V: TPoint).

В V содержатся координаты точки, координаты которой надо преобразовать.

В F содержатся результат.

M - матрица преобразования.

В процедуру Ray передается только матрица перехода из глобальной системы координат в систему, связанную с лучом (M_i ).

Процедура находит координаты вторичного луча в новой системе координат.

Составляет матрицу перехода из текущей системы в систему, связанную с лучом (L_{i +1} ).

Умножает матрицы M_{i +1} =L_{i +1} M_i

Вызывает рекурсивно Ray с параметром M_{i +1}

2.3. 5 Определение пересечения луча с треугольником

Преобразуем все вершины треугольника в локальную систему координат, связанную с лучом. Луч в этой системе координат имеет координаты (0, 0,1). После этого задача сводится плоской. Необходимо определить, лежит ли точка (0, 0) внутри треугольника в проекции на плоскость OXY.

Преобразуем координату x вершин треугольника в локальную систему координат.

Проверяем, лежат ли точки треугольника все справа от нуля или все слева. Если да, то пересечения с треугольником нет. Если нет, то:

Преобразуем координату у вершин треугольника в локальную систему координат.

Проверяем, лежат ли точки треугольника все сверху от нуля или все снизу. Если да, то пересечения с треугольником нет. Если нет, то:

Необходимо, чтобы при обходе треугольника по часовой стрелке точка (0,0) лежала справа от каждой стороны (либо наоборот). Это можно установить, проверив одного ли знака три векторных произведения:

, , .

Если не одного знака, то пересечения нет, Если одного, то:

Преобразуем координату z вершин треугольника в локальную систему координат.

Определяем нормаль к треугольнику, для этого умножим векторно два вектора

и