Курсовая работа: Реализация алгоритма обратной трассировки лучей для моделей с большим числом полигонов

В случае если, NZ равно нулю, луч параллелен оси OZ и соответственно лучу. Значит, пересечения нет. В другом случае пересечение есть.

Находим координаты пересечения.

Составим уравнение плоскости, в которой находится треугольник:

,

подставим x=0 и y=0,

2.3.4 Формирование отраженного луча

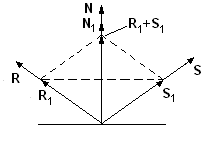Обозначим отраженный луч через R, вектор, направленный против падающего луча - S, вектор нормали - N. Рассмотрим единичные векторы этих векторов R₁ , S₁ , N₁ . Так как все три вектора находятся в одной плоскости, то можно записать R₁ +S₁ =N^’ . Длина вектора N^’ равна 2cosθ. Так как векторы N^’ и N₁ сонаправленные, то можно записать:

N’=N₁ 2cosθ.

Таким образом

.

Поставим условие, что падающий и отраженный лучи имеют одинаковую длину.

Так как падающий луч в локальной системе координат имеет координаты (0, 0,1). То вектор S будет иметь координаты (0, 0, - 1). Подставим его координаты в выражение для отраженного луча. Получим

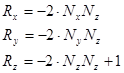
2.3.5 Формирование преломленного луча

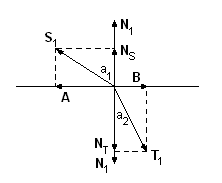Обозначим преломленный луч, имеющий единичную длину, через T₁ . Единичный вектор нормали - через N₁ . А вектор, направленный противоположно падающему лучу - через S₁ . Разложим вектор S₁ на A и N_s , а вектор T₁ на B и N_T . Вектор равен

.

Найдем вектор N_T . Этот вектор противоположен по направлению вектору нормали, а длина его равна

.

Таким образом

.

Для того, что бы определить cosα₂ , запишем закон преломления

.

Воспользуемся тождеством

Получим