Курсовая работа: Решение дифференциального уравнения первого порядка

Из полученных формул исключим члены, содержащие и .

Для этого вторую формулу умножим на , а третью – на и сложим с первой. Будем иметь:

Таким образом, с точностью до имеем приближённую формулу

(3)

Можно показать, что остаточный член формулы (3) равен где Аналогично имеем:

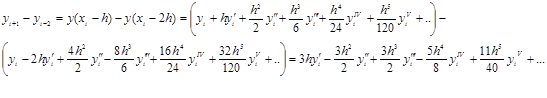и

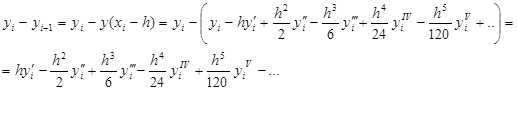
Отсюда

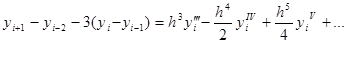
С другой стороны

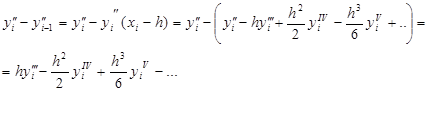
Поэтому

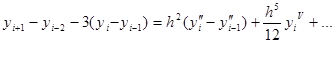
Таким образом, с точностью до h⁵ имеем приближённую формулу

(4)

Можно доказать, что остаточный член формулы (4) есть

где

К формулам (3) и (4) присоединим выражения для производных:

(5)

(6)

Процесс численного дифференцирования уравнения (1) при наличии начального условия (2), использющий формулы (3) и (4), происходит следующим образом. Каким-либо методом вычисляем три начальные строки (начальная таблица):

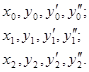
Из формулы (4) при i=2 получаем первое приближение для :

(7)