Курсовая работа: Решение дифференциального уравнения первого порядка

1. Метод Адамса

Этот метод численного интегрирования разработан Адамсом в 1855г. В последствии этот метод был забыт и вновь открыт в начале века. Популяризация метода Адамса и дальнейшее его усовершенствование связаны с именем А.Н. Крылова.

Изложим метод Адамса применительно к уравнению первого порядка

(1)

с начальным условием

(2).

Пусть x(i=0,1,2,….) – система равностоящих значений с шагом h и =. Очевидно, имеем

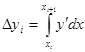(3).

В силу второй интерполяционной формулы Ньютона с точностью до разностей четвертого порядка получаем

(4)

где .

Подставляя выражение (4) в формулу (3) и учитывая, что dx=hdq, будем иметь

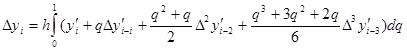
Отсюда получаем экстраполяционную формулу Адамса

. (5)

Для начала процесса нужны четыре начальных значения , так называемый начальный отрезок, который определяют исходя из начального условия (2), каким-нибудь численным методом. Можно, например, использовать метод Рунге-Кутта. Зная эти значения, из уравнения (1) можно найти значения производных и составить таблицу разностей.

(6)

Дальнейшие значения (i=4,5,…) искомого решения можно шаг за шагом вычислять по формуле Адамса, пополняя по мере необходимости таблицу разностей (6).

Для контроля рекомендуется вычислив первое приближение для по формуле

определить , подсчитать конечные разности.

, , (7)

и затем найти второе приближение по более точной формуле

(8)

Если и отличаются лишь на несколько единиц последнего сохраняемого десятичного разряда, то можно положить , а затем, найдя , перевычислив конечные разности (7). После этого, строго говоря, следует снова найти по формуле(8). Поэтому шаг h должен быть таким , чтобы этот пересчёт был излишним.

На практике шаг h выбирают столь малым, чтобы можно было пренебречь членом в формуле (8).

Если же расхождение величин и значительно, то следует уменьшить шаг h.

Обычно шаг h уменьшают в два раза. Покажем, как в этом случае, имея до некоторого значения i таблицу величин и, (ji) c шагом , можно просто построить таблицу величин (k=0,1,2…) с шагом . Для кратности введения сокращенные обозначения:

(k=0,1,2…).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--