Курсовая работа: Решение прикладных задач численными методами

ЦЕЛЬ РАБОТЫ:

Получение практических навыков по применению численных методов при решении прикладных задач на ЭВМ общего назначения, с использованием программ сложных циклических алгоритмов, включая редактирование программ в ЭВМ, отладку программ, выполнение расчетов на периферийные устройства.

Время: 12 часов.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Работа состоит из 2-х частей.

Цель первой части курсовой работы: получить практические навыки в использовании численных методов решения не линейных уравнений используемых в прикладных задачах.

Для выполнения 1 части работы необходимо:

· Составить программу и рассчитать значения функции в левой части нелинейного уравнения для решения задачи отделения корней;

· Составить логическую схему алгоритма, таблицу идентификаторов и программу нахождения корня уравнения методом дихотомии и методом, указанным в таблице;

· Ввести программу в компьютер, отладить, решить задачу с точностью ε_=0,0001 и вывести результат;

· Предусмотреть в программе вывод на экран дисплея процессора получения корня.

Задание на выполнение первой части курсовой работы:

Вариант №21.

Уравнение: 0,25 x ³ + x -1,2502=0:

Отрезок, содержащий корень: [0;2].

I. Математическое описание численных методов решения

Метод деления отрезка пополам (метод дихотомии).

Этот метод позволяет отыскать корень уравнения с любой наперёд заданной точностью εε . искомый корень x уравнения уже отделен, т.е.указан отрезок [а, в] непрерывности функции f ( x ) такой, что на концах этого отрезка функция f(x) принимает различные значения:

f ( a )* f ( b )>0

В начале находится середина отрезка [ a, b ]:

и вычисляется значение функции в точке с, т.е. находится f ( c ). Если f ( c )=0, то мы точно нашли корень уравнения. Если же f ( c )≠0 ,то знак этой величины сравнивается со знаками функции y = f ( x ) в концах отрезка [ a, b ]. Из двух отрезков [ a, с], [ с, b ] для дальнейшего рассмотрения оставляется тот, в концах которого функция имеет разные знаки. С оставленным отрезком поступаем аналогичным образом. расчет прекращается, когда оставленный отрезок будет иметь длину меньше 2ε. В этом случае принимаем за приближенное значение корня середину оставленного отрезка и требуемая точность будет достигнута.

II. График функции.

Для выделения корней рассчитаем значения функции на заданном отрезке [0,2] с шагом 0,0001 и по полученным данным построим график функции.

Как видно из рисунка график пересекает ось Х один раз, следовательно, на данном отрезке [ 0, 2] наше уравнение имеет один корень.

Алгоритмы нахождения корней уравнения

I . C труктурная схема алгоритма: Метод дихотомии

f(a0 ), f(b0 )

да

		x=c
		an+1 =an ; bn+1 =c					an+1 = c ; bn+1 = bn
n=n+1
X = a n +b n 2

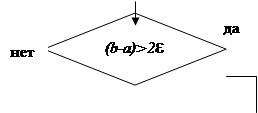Листинг программы имеет вид

--> ЧИТАТЬ ПОЛНОСТЬЮ <--