Курсовая работа: Решение прикладных задач численными методами

Метод решения: метод Эйлера-Коши, Δx = 0,01; 0,005; 0,001.

Метод Эйлера-Коши

Метод Эйлера-Коши (или усовершенствованный метод Эйлера) является методом второго порядка и заключается в следующем. Интегральная кривая на каждом шаге интегрирования заменяется прямой с тангенсом угла наклона, равным среднему арифметическому тангенсов углов наклона касательных к искомой функции в начале и в конце шага. Вычисления проводятся в следующем порядке:

1. Выбираем шаг интегрирования .

2. Полагаем номер шага .

3. Вычисляем , находим оценку для приращения функции на этом шаге методом Эйлера , , вычисляем среднее арифметическое тангенсов углов наклона и окончательно получаем:

.

4. Если , то увеличиваем номер шага на единицу и повторяем п.3. В противном случае переходим к выполнению п.5.

5. Оформляем полученный результат.

Достоинство метода – более высокая точность вычисления по сравнению с методом Эйлера. Недостаток – больший объем вычислений правых частей.

Таблица идентификаторов :

Обозначение	Идентификатор	Тип
s	s	int
i	i	int
x	x	float
xmax	x_max	float
x1	x1	float
Δx	h[i]	float
y	y	float
d	d	float
f(x)	f(x)	float
k	k(x,y)	float
K1	f1	float
K2	f2	float
K3	f3	float
K4	f4	float

Схема алгоритма :

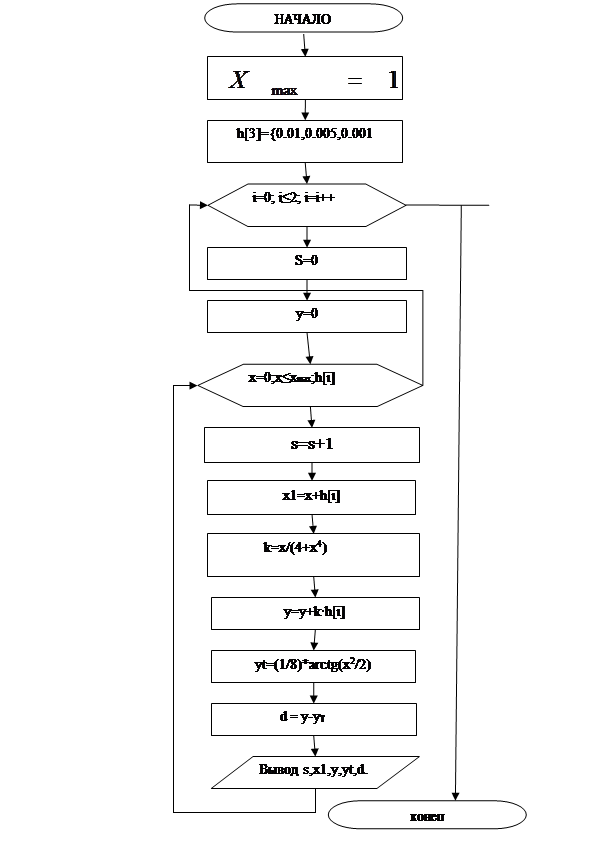
6. Листинг программы:

#include<stdio.h>

#include<math.h>

int s,i;

double x, x1, x_max=2, y, d, q;

double h[3]={0.01,0.005,0.001};

double k(double x,double y )

{

return ((x)/(4+(pow(x,4))));

}

double e(double x)

{

return 0.25*atan(pow(x,2)/2);

}

double f1=k(x,y);

double yw=y+f1*h[i];

double r=x+h[i];