Курсовая работа: Решение транспортных задач

Данная функция, определяющая суммарные затраты на все перевозки, должна достигать минимального значения.

Составим систему ограничений задачи. Сумма всех перевозок, стоящих в первой строке матрицы Х, должна равняться запасам первого поставщика, а сумма перевозок во второй строке матрицы Х – запасам второго поставщика:

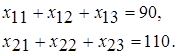
Это означает, что запасы поставщиков вывозятся полностью.

Суммы перевозок, стоящих в каждом столбце матрицы Ч, должны быть равны запросам соответствующих потребителей:

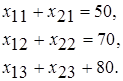
Это означает, что запросы потребителей удовлетворяются полностью.

Необходимо также учитывать, что перевозки не могут быть отрицательными:

i=1,2,…,m; j=1,1,…,n.

Ответ: математическая модель задачи формулируется следующим образом: найти переменные задачи, обеспечивающие минимум функции

и удовлетворяющие системе ограничений

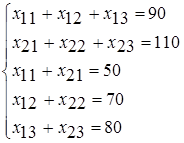
и условиям неотрицательности

i=1,2,…,mj=1,2,…,n.

1.2 АЛГОРИТМ РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ

1.2.1 СБАЛАНСИРОВАННОСТЬ ТРАНСПОРТНОЙ ЗАДАЧИ

Транспортная задача является сбалансированной, если суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.

.

Если транспортная задача не сбалансирована, то возникают особенности в ее решении.

Особенности решения транспортных задач с неправильным балансом:

1.Если суммарные запасы поставщиков превосходят суммарные запросы потребителей, т.е.

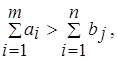
то необходимо ввести фиктивного (n+1)-го потребителя с запросами 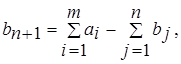равными разности суммарных запасов поставщиков и запросов потребителей, и нулевыми стоимостями перевозок единиц груза

2. Если суммарные запросы потребителей превосходят суммарные запасы поставщиков, т.е.

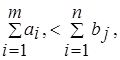
то необходимо ввести фиктивного (m+1)-го поставщика с запасами 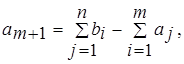равные разности суммарных запросов потребителей и запасов поставщиков, и нулевыми стоимостями перевозок единиц груза

3. При составлении начального опорного решения в последнюю очередь следует распределять запасы фиктивного поставщика и удовлетворять запросы фиктивного потребителя, несмотря на то, что им соответствует наименьшая стоимость перевозок, равная нулю.

1.2.2 ОПОРНОЕ РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ