Курсовая работа: Ряды Фурье. Численные методы расчета коэффициентов

Теперь через полученные указанным путем величины k, l, m, n, q и r коэффициентов Фурье выразятся следующим образом:

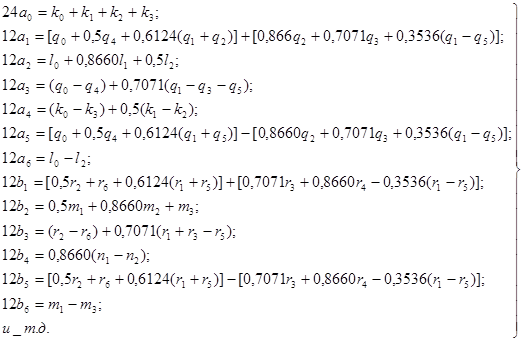
Дальнейшие коэффициенты по двадцати четырем ординатам получаются с все меньшей точностью.

Нужно обратить внимание на одну подробность. Для получения коэффициентов и нужно отдельно вычислить те выражения, которые поставлены в квадратные скобки, а затем сложить их (для нахождения ) и вычесть (для нахождения ). Аналогичное замечание – относительно вычисления коэффициентов и .

3.1.2. Быстрое преобразование Фурье.

Тригонометрическая интерполяция. Дискретное преобразование.

Дискретное преобразование Фурье применяется при решении многих прикладных задач. К ним относится тригонометрическая интерполяция, вычисление сверстки функций, распознавание образов и многие другие. Дискретное преобразование Фурье стало особенно эффективным методом решения прикладных задач после создания быстрого преобразования Фурье.

Пусть f(x) – периодическая функция с периодом 1 – разложена в ряд Фурье

, (1)

причем

. (2)

Здесь i – мнимая единица.

Рассмотрим значение этой функции на сетке из точек , где l, N целые, N фиксировано, и обозначим . Если , где k целое, то , где kl целое. Следовательно,

(3)

в узлах сетки. Поэтому если функция f(x) рассматривается в узлах сетки , то в соотношении (1) можно привести подобные члены

, (4)

где

. (5)

Лемма. При , определяемых (5), соотношение (4) остается в силе, если пределы суммирования [0, N-1] заменить на [m,N-1+m], где m – любое целое.

Если с самого начала была задана функция, определенная только на сетке, то на этой сетке ее можно также представить в форме (1). Действительно, такую функцию можно продолжить на всю прямую, доопределив ее между узлами сетки путем линейной интерполяции. Для непрерывной кусочно-дифференцируемой функции выполняется (2), поэтому в точках сетки после приведения подобных членов получим (4).

Определим скалярное произведение для функции на сетке следующим образом:

.

(Множитель введен для согласованности получаемых соотношений с непрерывным случаем: если f(x) и g(x) – непрерывные функции на отрезке [0,1], то вследствие интегрируемости f(x)g(x) по Риману

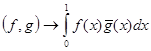
при ). Функции при образуют ортогональную систему относительно введенного таким образом скалярного произведения. Действительно,

.

При , суммируя геометрическую прогрессию, имеем

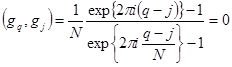
(при знаменатель отличен от 0). Поскольку , то в итоге имеем