Курсовая работа: Ряды Фурье. Численные методы расчета коэффициентов

,

где

.

Непосредственное вычисление всех требует арифметических операций, а последующее вычисление - еще операций. Поэтому при общее число операций составит . Точно так же при строится алгоритм вычисления совокупности значений , для которого общее число операций не превосходит , здесь С – постоянная, не зависящая от N. Выпишем соответствующие расчетные формулы для наиболее употребительного случая . Представим числа q, l в виде

,

где . Величину представим в виде

,

где s - целое, равное сумме всех слагаемых вида , которых . Очевидно, что , поэтому

После перегруппировки слагаемых имеем

Это соотношение можно записать в виде последовательности рекуррентных соотношений

где

Переход от каждой совокупности к совокупности требует O(N) арифметических и логических операций; всего таких шагов r, поэтому общее число операций имеет порядок .

Вычисление при помощи совокупностей дает меньшее накопление вычислительной погрешности по сравнению с формулами (3.7). Определенные удобства имеются также при вычислении экспонент, входящих в расчетные формулы. При вычислении величин используются значения , . В частности, при m=1 величина принимает значения +1 или -1. Для вычисления значений потребуются еще значения при нечетных j, удовлетворяющих неравенству . Их можно вычислить через уже вычисленные до этого величины, в частности, при помощи соотношений

где, в свою очередь,

при .

В ряде случаев удается еще уменьшить число операций. Один из таких случаев упоминался выше: дана вещественная функция , известная в точках ; требуется найти коэффициенты интерполяционного многочлена

.

Другой случай: при четном N заданы значения функции

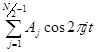
в точках ; нужно определить коэффици