Курсовая работа: Ряды Фурье. Численные методы расчета коэффициентов

Умножая (4) скалярно на , получим равенство

(7)

Выражение в правой части образует квадратурную сумму для интеграла

,

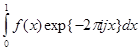поэтому

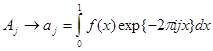
при и фиксированном j.

Покажем, что соотношение

(8)

в общем случае не имеет места. Пусть . Из (4) получаем , остальные . Таким образом, правая часть (8) есть . Она совпадает с f(x) в точках , но, как правило, далека от нее вне этих точек.

Воспользовавшись утверждением леммы, перепишем (4) в виде

. (9)

Если f(x) – достаточно гладкая функция, то величины с ростом j убывают быстро, поэтому при малых q. Кроме того, при гладкой f(x) величины и малы при больших q.

Напомним, что это приближенное равенство обращается в точное равенство в точках сетки. Способ аппроксимации

Носит название тригонометрической интерполяции. Соотношение (9) называют конечным или дискретным рядом Фурье, а коэффициенты - дискретными коэффициентами Фурье.

Игнорирование установленного нами факта о равенстве функций и в узлах сетки при часто являются источником получения неверных соотношений.

Существует соответствие между задачей приближения функций линейными комбинациями Чебышева и тригонометрическим многочленами. Пусть на отрезке [-1,1] функция f(x) приближается линейными комбинациями . Замена переменных x=cost сводит исходную задачу к задаче приближения функции f(cost) линейной комбинацией .

Справедливо равенство

.

Следовательно, задача наилучшего приближения f(x) в норме, соответствующей скалярному произведению , эквивалентна задаче приближения в норме, соответствующей скалярному произведению . Точно так же существует соответствие в случае задач интерполяции и наилучшего приближения в равномерной метрике. Задача интерполирования функции многочленом по узлам - нулям многочлена Чебышева - после такой замены сводится к задаче интерполирования функции f(cost) при помощи тригонометрического многочлена по узлам , образующим равномерную сетку.

3.1.2.3. Быстрое преобразование Фурье.

Осуществление прямого и обратного дискретных преобразований Фурье

Является составной частью решения многих задач решения многих задач. Непосредственное осуществление этих преобразований по формулам (4), (7) требует арифметических операций. Рассмотрим вопрос о возможности сокращение этого числа. Для определенности речь пойдет о вычислении коэффициентов по заданным значениям функции. Идея построения алгоритмов быстрого преобразования Фурье опирается то, что при составном N в слагаемых правой части (7) можно выделить группы, которые входят в выражения различных коэффициентов . Вычисляя каждую группу только один раз, можно значительно сократить число операций.

Рассмотрим сначала случай . Представим q, j, лежащие в пределах , в виде , где . Имеем цепочку соотношений

.

Из равенства