Курсовая работа: Рішення систем нелінійних рівнянь. Метод ітерацій. Метод Ньютона–Канторовича

y ^{(1 )} =0.842-1.32=-0.478

x ^{(2 )} =0.888+0.85=1.738

y ^{(2 )} =0.961-1.32=0.359

x ^{(3 )} =0.936+0.85=1.786

y ^{(3 )} =0.986-1.32=0.334

x ^{(4 )} =0.945+0.85=1.795

y ^{( 4)} =0.977-1.32=0.343

x ⁽⁵⁾ =0.9408+0.85=1.7908

y ⁽⁵⁾ =0.9750-1.32= - 0.3450

x ^{(6 )} = 0.9411+0.85=1.7911

y ^{(6 )} = 0.9759-1.32=0.3441

x ^{( 7)} = 0.9414+0.85=1.7914

y ^{( 7)} = 0.9758-1.32=-0.3442.

1.2 Метод найшвидшого спуску

Нехай маємо систему рівнянь:

або в матричному вигляді:

де

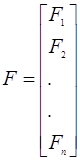
Допустимо, що функція дійсно непереривна та непреривно диференційована в загальній області визначення. Розглянемо функцію

Тоді рішення даної системи зводиться до мінімізації цієї функції.

Для мінімізації по методу спуску вибирається початковий вектор Х⁰ , а потім шукається напрямлення спуска до рішення , таке щоб

для векторів Х ⁽¹⁾ виду . Тут - скалярна величина, постійна для даної ітерації і знаходить величину шагу за напрямом .

Методи спуску розрізняються в залежності від вибору напрямлення спуска. Одним із найкращих направлень є напрямлення градієнта

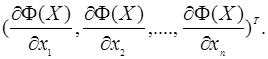
Функція Ф (Х ^(і)) задається в n-мірному просторі сімейства гіперповерхонь і градієнт вирішує напрям найшвидшого спуска. Тому саме воно використовується у методі найшвидшого спуска для мінімізації функції.

Другою проблемою в методах найшвидшого спуску є вибір величини шагу , на який потрібно про двинутися вздовж напряму зменшення функції.