Курсовая работа: Рішення систем нелінійних рівнянь. Метод ітерацій. Метод Ньютона–Канторовича

для якого функція приймає менше значення, чим . Розкладемо функцію

в ряд Тейлора та обмежившись членами другого порядку меншості получимо

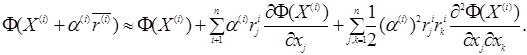(3)

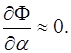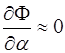Тоді значення , для якого функція прийме мінімальне значення, визначається із умови Про диференціювавши рівняння (3) по і враховуючи, що получимо

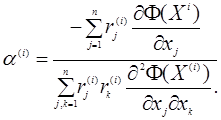(4)

Оскільки в методі найшвидшого спуску компоненти градієнта мають вигляд

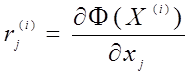
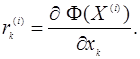
то формула (4) після підстановки цих рівнянь перейде до вигляду

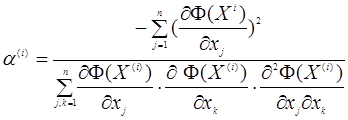(5)

Формула (5) дуже складна оскільки потребує рахування других часних похідних.

На практиці завжди використовується наступний варіант знаходження .

Нехай значення Ф (Х) змінюється вздовж напрямку градієнта . Розглянемо точку пересікання кривої та касатільної в точці з осю .

Вона буде розраховуватися наступним чином:

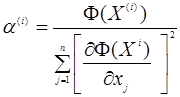. (6)

Як бачимо, в цьому випадку рахується просто, але сходження метода може бути дуже повільно. Тому інколи на практиці використовують наступну модифікацію.

Для кожної ітерації метода рахують значення функціонала при , а потім при і будують квадратичне наближення функціонала, який проходить через три точки 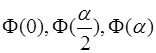. Продиференціювавши отримане рівняння по та прирівнявши похідну, получимо наступне рівняння для

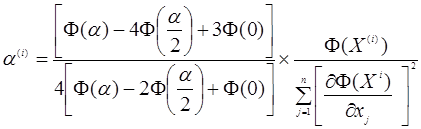(7)

Практика показує, що хоча цей варіант більш громіздкий, так як у порівнянні з формулою (5) доводиться додатково рахувати два значення функції 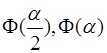, але метод сходиться набагато швидше.

Інколи характер Ф (Х) такий, що аналітичне рівняння для частних похідних має надто складний вигляд і рахувати їх надто складно.

Також слід відмітити, що якщо в області шуканого рішення є локальні мінімуми, то метод спуска може не привести до шукаємого рішення, а можуть зійтися до одного з цих мінімумів. Практично часто спуск буває дуже повільним навіть при відсутності локальних мінімумів.

Порядок рахування в методі найшвидшого спуска наступний:

знаходиться аналітичне рівняння для градієнта ;

вибирають початкове приближення вектора невідомих ;

вираховують координати градієнта в точці ;

вираховують шаг по градієнту по формулам (6) або (7);

вираховують уточнений вектор невідомих .