Курсовая работа: Рішення систем нелінійних рівнянь. Метод ітерацій. Метод Ньютона–Канторовича
Методом найшвидшого спуска приблизно розрахувати корені системи
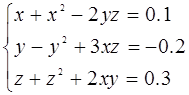
розміщенні в області початку координат.
Маємо:
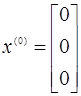 Тут
Тут 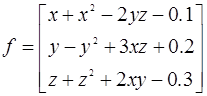 та
та
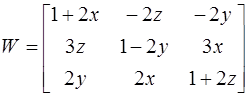
Підставляємо нульове приближення, будемо мати:
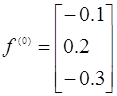 та
та 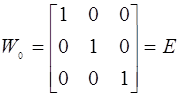
по формулам получимо перше приближення
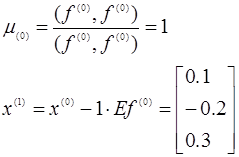
Аналогічно находимо друге приближення ![]() . Маємо:
. Маємо:
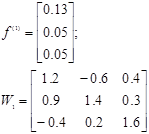
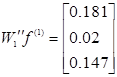
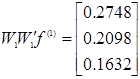
![]()
![]()

 .
.
1.3 Метод Ньютона-Канторовича
Метод Ньютона-Канторовича, придатний для проведення розрахунків в Excel. Як і в методі Ньтона для нелінійних рівнянь для знаходження кореня системи нелінійних рівнянь необхідно спочатку якимсь чином знайти початкове наближення до цього кореня (тобто вектор
 ),
),
а потім вже використовуються ітераційні формули методу проводиться його уточнення до досягнення заданої точності. Виклад методу (і його використання) зручніше проводити в матричній формі запису. При цьому, окрім векторів, ![]() ,
, ![]() и
и ![]() (. (i - номер ітерації,, i ³ 0) ) використовується також матриця A (розмірності n ´ n), що складається з приватних похідних по всіх компонентах вектора
(. (i - номер ітерації,, i ³ 0) ) використовується також матриця A (розмірності n ´ n), що складається з приватних похідних по всіх компонентах вектора ![]() :
:
 :
:
Розглянемо ці методи для випадку n=2, тобто коли рівнянь в системі два і невідомих теж дві. В цьому випадку
 , та
, та  .
.
Ідея методу полягає в розкладанні вектор-функції в ряд Тейлора в околиці початкового наближення із збереженням тільки доданків першого ступеня. Позначимо найдене (якимсь чином) початкове приближення до шуканого кореня через  . Тоді можна приблизно записати
. Тоді можна приблизно записати
 , (8)
, (8)
На основі формула (8) будується ітараційна формула. А саме, ![]() вибирається так, щоб
вибирається так, щоб ![]() .
.
Тоді (у загальному вигляді) ітераційна формула матиме вигляд
![]() (9)
(9)
В методі Ньютона цю ітераційну формулу перетворять до вигляду