Курсовая работа: Розрахунок елементів цифрової системи передачі інформації
Математичне сподівання визначається
 (1.2)
(1.2)
Дисперсія визначається
 (1.3)
(1.3)
Середня квадратична похибка:
![]() (1.4)
(1.4)
З отриманого виразу одномірної щільності ймовірності миттєвих значень повідомлення х (t ) будуємо випадковий процес (рисунок 1.2). У даному випадку побудовано графік із 10 випадкових точок:
|
|

Рисунок 1.2 – Випадковий процес
2. Кодер джерела
Визначення інтервалу дискретизації повідомлення х (t ) за часом проведено за формулою:
![]() (2.1)
(2.1)
Крок квантування визначається:
![]() (2.2)
(2.2)
Середня потужність шуму квантування:
 (2.3)
(2.3)
Відношення середньої потужності шуму квантування до середньої потужності сигналу:
![]()
Число розрядів вихідної кодової комбінації АЦП:
![]() (2.4)
(2.4)
![]()
Двійкові кодові комбінації, що відповідають L рівням квантування, приведені у таблиці 2.1
Таблиця 2.1 – двійкові кодові комбінації, що відповідають L рівням квантування
| N з/п | x(tk ), В | Кодова комбінація |
| 1 | -1,6 | |
| 2 | -1,173 | |
| 3 | -0,746 | |
| 4 | -0,319 | |
| 5 | 0,108 | |
| 6 | 0,535 | |
| 7 | 0,962 | |
| 8 | 1,389 | |
| 9 | 1,816 | |
| 10 | 2,243 | |
| 11 | 2,67 | |
| 12 | 3,097 | |
| 13 | 3,524 | |
| 14 | 3,951 | |
| 15 | 4,378 | |
| 16 | 4,805 |
Ентропія джерела дискретних повідомлень
![]() (2.5)
(2.5)
а оскільки повідомлення рівно ймовірні і
![]() ,
,
то ентропію можна визначити як
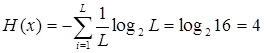 (біт/повідомлення) (2.6)
(біт/повідомлення) (2.6)
Число двійкових символів, що видає АЦП в одиницю часу: