Курсовая работа: Розрахунок інтегралів за допомогою методів Гауса та Чебишева

Розроблена програма дозволяє розрахувати вказаний інтеграл:

,

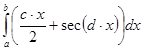методами Чебишева та Гауса з кроками 0,1 і 0,05.

Результати виводяться у текстовій формі.

4. Розробка та опис логічної частини програми

В даній курсовій роботі було розроблено програмне забезпечення для розв’язання та дослідження заданого диференційного рівняння. Розвязок ведеться за різницевим алгоритмом. Кодування на мові Паскаль проводилося з застосуванням інтуїтивно-зрозумілих назв змінних та процедур. Також відступи та табуляція дозволяє досить легко збагнути структуру програми.

В інтерфейсі також не допущено зайвих елементів.

5. Керівництво оператору

Для завантаження програми необхідно запустити програмний файл Project1.exe. При цьому зявиться вікно (рис. 1), де можна задати початкові умови, переглянути постановку задачі а також ознайомитися з розв’язком при натисненні кнопки Розвязок.

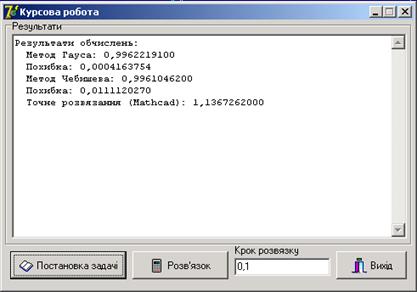
Рисунок 1. Інтерфейс програми.

6. Результати обчислень

Результати обчислень:

Метод Гауса: 0,9962219100

Похибка: 0,0004163754

Метод Чебишева: 0,9961046200

Похибка: 0,0111120270

Точне розвязання (Mathcad): 1,1367262

Висновки

При виконані даної курсової роботи я навчилась розраховувати інтеграли за допомогою методів Гауса та Чебишева. Було відмічено, що метод Гауса є значно точнішим від Чебишева, за що і отримав назву метода найвищої математичної точності.

Література

1. Самарський А.А. Вступ в чисельні методи. - М.: Наука,

1987. – 286 с.

2.Квєтний Р.Н., Маліков В.Т. Обчислювльні методи та використання ЕОМ. Вища школа, 1989 – 55 с., 104 с.

Додаток A – Алгоритм роботи програми

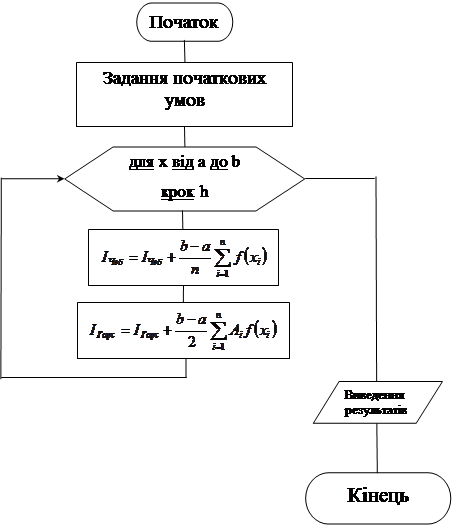Додаток Б - Лістинг програми

unit Unit1;

interface

uses