Курсовая работа: Розрахунок стрижневої системи зі скінченним числом ступенів свободи на вільні та вимушені коливання

Отже, перевірки для всіх форм коливань виконані й умова ортогональності задовільняється.

2. Розрахунок на вимушені коливання

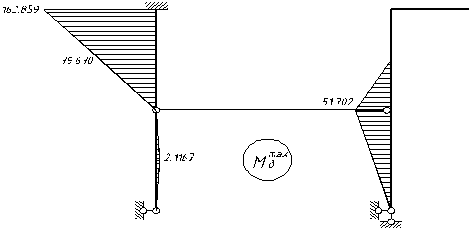
2.1 Розрахункова схема

n=q/ω₁ =0,82;

2.2 Запис рівняння вимушених коливань при частоті

1). Запишемо диференційне рівняння вимушених коливань. Так як сили опору коливанням не враховуються, то переміщення при вимушених коливаннях будуть залежати від сил інерції і збурюючої сили:

Рішення системи шукаємо для випадку стаціонарних коливань. Вважаємо, що всі маси коливаються за законом збурюючої сили:

у_і =c_і sinθt;= -c_і θ² sinθt,

с_і - амплітуда переміщень в і-му напрямку.

В цьому разі:

2). Обчислимо вільні члени шляхом побудови епюри згинальних моментів від амплітудного значення збурюючої сили:

Визначимо одиничні переміщення мас під дією зовнішнього навантаження:

;

;

.

Для перевірки правильності обчислення вільних членів, знайдемо добуток сумарної епюри від одиничного навантаження та епюри моментів від амплітудного значення збурюючої сили:

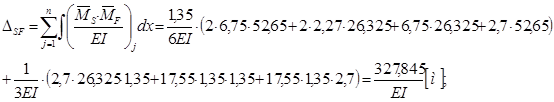
Оскільки =, то вільні члени визначено вірно.

2.3 Вихідні дані для розрахунку вимушених коливань на ЕОМ

Співвідношення частот вимушених і вільних коливань:

q/ω₁ =0,82; Вектор вільних членів: .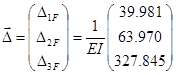

2.4 Обчислення амплітуд сил інерції та амплітуди коливань

Розв’язавши систему рівнянь за допомогою програми Dinamo16, одержимо: амплітуди сил інерції: Z₁ = 2,606116 [кН], Z₂ = 3.135882 [кН], Z₃ = 25.298055 [кН]. Амплітуди коливань: С₁ = 123.137351/ЕІ [м], С₂ = 197.557959/ЕІ [м], С₃ = 683.038443/ЕІ [м].

2.5 Побудова епюри згинальних моментів від дії динамічних навантажень та її кінематична перевірка

.