Курсовая работа: Розробка математичної програми в середовищі С++

, (17)

який збігається при

. (18)

Якщо в деякому околі кореня виконуються умови

, (19)

то метод релаксації збігаються при . Збіжність буде найкращою при

. (20)

При такому виборі t для похибки буде мати місце оцінка

, (21)

де .

Кількість ітерацій, які потрібно провести для знаходження розв’язку з точністю e визначається нерівністю

. (22)

Зауваження: якщо виконується умова , то ітераційний метод (17) потрібно записати у вигляді .

Метод Ньютона

Метод Ньютона застосовується до розв’язування задачі (1), де f(x) є неперервно-диференційованою функцією. На початку обчислень вибирається початкове наближення x₀ . Наступні наближення обчислюються за формулою

. (23)

З геометричної точки зору x_n+1 є значенням абсциси точки перетину дотичної до кривої y=f(x) в точці (x_n , f(x_n )) з віссю абсцис. Тому метод Ньютона називають також методом дотичних.

Теорема 2. Якщо не змінює знака на [a, b], то виходячи з початкового наближення , що задовольняє умові , можна обчислити методом Ньютона єдиний корінь рівняння (1) з будь-якою степінню точності.

Теорема 3. Нехай - простий дійсний корінь рівняння (1) і , де ,

, (24)

причому

. (25)

Тоді для метод Ньютона збігається, причому для похибки справедлива оцінка

. (26)

З оцінки (26) видно, що метод Ньютона має квадратичну збіжність, тобто похибка на (n+1) – й ітерації пропорційна квадрату похибки на n-й ітерації.

Модифікований метод Ньютона

(27)

дозволяє не обчислювати похідну на кожній ітерації, а отже і позбутися можливого ділення на нуль. Однак цей алгоритм має тільки лінійну збіжність.

Кількість ітерацій, які потрібно провести для знаходження розв’язку задачі (1) з точністю e задовольняє нерівності

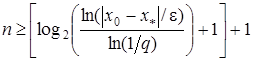. (28)