Курсовая работа: Семейства решений с постоянной четной частью

3. Система чет-нечет

Рассмотрим систему

(3.1)

Будем считать, что всюду в дальнейшем эта система удовлетворяет условиям:

а.) Функция непрерывно дифференцируема, и поэтому, задача Коши для системы (3.1) имеет единственное решение;

б.) Правая часть системы (3.1) – периодична по .

Лемма. Пусть система (3.1) удовлетворяет условиям а) . и б). Тогда продолжимое на отрезок решение этой системы будет – периодическим тогда и только тогда, когда

,

где – есть нечетная часть решения .

Пусть – – периодическое решение системы (3.1). Тогда . Необходимость доказана.

Пусть – решение системы (3.1), для которого . Тогда , и поэтому . Таким образом, точка есть неподвижная точка отображения за период, а решение – – периодическое.

Доказанная лемма вопрос о периодичности решения , сводит к вычислению одного из значений нечетной части. Иногда относительно можно сказать больше, чем о самом решении . Это позволяет в таких случаях делать различные заключения относительно существования периодических решений у систем вида (3.1). Дифференцируемые функции ; , удовлетворяют некоторой системе дифференциальных уравнений. Прежде, чем выписать эту систему, заметим:

(3.2)

Так как решение системы (3.1). Заменяя в тождестве (3.2) на и учитывая, что производная четной функции – функция нечетная, а производная нечетной функции – функция четная, получаем тождество

(3.3)

Из тождеств (3.2) и (3.3) найдем производные:

;

.

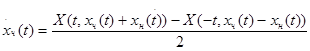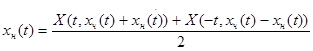Таким образом, вектор-функция

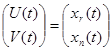(3.4)

Удовлетворяет следующей системе дифференциальных уравнений порядка

: ;

При этом . Систему (3.5) будем называть системой чет-нечет, соответствующей системе (3.1) решение системы чет-нечет, как следует из условия а), однозначно определяется своими начальными условиями.

4. Примеры систем, семейства решений которых имеют постоянную четную часть

1 .

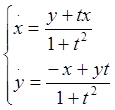
Найдем решение:

;