Соответственно, одного наблюдения недостаточно, чтобы сде­лать вывод о наличии синхронизации. Синхронизация — это слож­ ный динамический процесс, а не состояние [1].

7. Синхронизация: обзор различных случаев

Перечислим различные формы синхронизации без учета природы колебаний (т.е. генериру­ются ли они электронным устройством или живой клеткой) и природы связи (т.е. осуществляется ли она за счет механического соединения или диффузии реагентов химической реакции), т.е. оста­новимся на общих свойствах: являются ли колебания периодически­ми или нерегулярными; является ли связь взаимной или однонапра­вленной и т.д.Это не будет полной и строгой классификацией, а просто кратким обсуждением основных проблем теории синхрони­зации.

7. 1. Синхронизация внешней силой

Синхронизация была открыта Гюйгенсом как побочный результат его усилий по созданию высокоточных часов. В наши дни этот эффект используется для точного и недорогого измерения времени с помощью радиоуправляемых часов. В этом случае передаваемый порадио слабый сигнал от центральных высокоточных часов ежеми­нутно подстраивает ритм других часов, темсамым захватывая.

Похожая схема синхронизации была «реализована» природой для подстройки биологических часов, которые регулируют суточные (циркадные) и сезонные ритмы живых систем, от бактерии до че­ловека.

7. 2. Ансамбли осцилляторов и колебательные среды

Во многих естественных ситуациях взаимодействуют более двух объектов. Если два осциллятора способны к подстройке ритмов, то можно ожидать такой способности и от большого числа осцилляторов. Такая система называется ансамблем взаимно связанных осцилляторов . При этом можно гово­рить о глобальной (каждый с каждым) связи. Бывают и другие ситуации, когда осцилляторы упорядочены в цепочки или решет­ки, где каждый элемент взаимодействует с несколькими соседями. Такие структуры типичны для созданных человеком систем, напри­мер, для решеток лазеров, но могут также встречаться и в природе. Эксперименты показывают, что соседние осцилляторы в цепочке часто подстраивают своичастоты и формируют син­хронные кластеры.

Достаточно часто мы не можем выделить отдельный колебатель­ный элемент внутри естественного объекта. Вместо этого мы долж­ны рассматривать систему как непрерывную колебательную среду, где также возможна синхронизация.

7. 3. Фазовая и полная синхронизация хаотических осцилляторов

В наши дни широко известно, что автоколебательные системы, на­пример нелинейные электронные цепи, могут генерировать довольно сложные, хаотические сигналы. Многие естественные системы также демонстрируют сложное поведение. Недавние исследования показывают, что при наличии связи такие системы также могут синхронизоваться. Конечно же, в этом случае нам необходимо уточ­нить понятие синхронизации, потому что совершенно не очевидно, как характеризовать ритм хаотического осциллятора. Иногда хаотические сигналы относительно просты, как, например, показанный на рисунке 3. Такой сигнал — «почти пе­риодический». Можно считать, что он состоит из похожих циклов с изменяющейся амплитудой и периодом (который может быть гру­бо определен как интервал между соседними максимумами). Выбрав большой интервал времени τ , мы можем сосчитать число циклов в этом интервале N _τ ,вычислить среднюю частоту

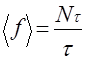(4)

и взять ее в качестве характеристики хаотического колебательного процесса [4].

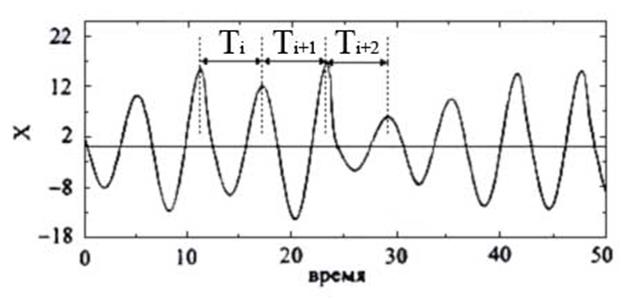
Рис.3. Пример хаотических колебаний.

С помощью средних частот мы можем описать коллективное поведение взаимодействующих хаотических систем точно так же, как и периодических. Если связь достаточно велика (например, для резистивно связанных электрических цепей это означает, что со­противление должно быть достаточно мало), средние частоты двух осцилляторов становятся равными. Важно отметить, что совпадение средних частот не означает, что сигналы также совпадают. Оказывается, что слабая связь не оказывает влияния на хаотическую природу обоих осцилляторов, их амплитуды остаются нерегулярными и некоррелированными, в то время как частоты подстраиваютсятаким образом, что мы можем говорить о фазовом сдвиге между сигналами. Такой режим называется фазовой синхронизацией хаотических систем .

Очень сильная связь стремится сделать состояния обоих осцил­ляторов идентичными. Она влияет не только на средние частоты, но также и на хаотические амплитуды. В результате, сигналы со­впадают (или почти совпадают) и наступает режим полной син­ хронизации .

Явление синхронизации может также наблюдаться в больших ан­самблях взаимно связанных хаотических систем и в сформирован­ных имипространственных структурах [1].

8. Цепочки осцилляторов

8. 1. Синхронизация N связанных осцилляторов

Рассмотрим синхронизацию N связанных осцилляторов на примере электронных генераторов, связанных через емкость, индуктивность и сопротивление. Уравнения колебаний в такой системе имеют вид:

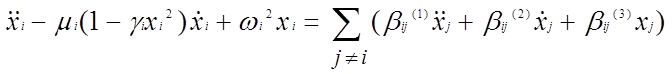(i=1,2,...,N). (5)

Здесь x_i – напряжения на входах усилителей, ω_i – собственные частоты колебательных контуров, μ_i – превышения над порогом генерации, β_ij ⁽¹⁾ – коэффициенты индуктивной связи, β_{i j} ⁽²⁾ – коэффициенты емкостной связи, β_ij ⁽³⁾ – коэффициенты связи через сопротивление, (1 – γ_i x_i ² ) – функции, характеризующие нелинейные свойства усилителей.

Будем считать, что частоты автономных генераторов близки друг к другу, тогда решение уравнения (5) можно искать в виде:

x_i =А_i cos(ωt+φ_i ), = – А_i ωsin(ωt+φ_i ), (6)

где ω=(1/N) .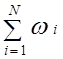

Для амплитуд и фаз получаем следующие уравнения:

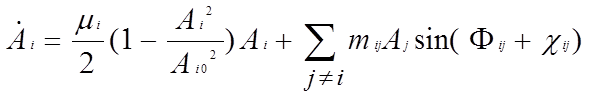(7)

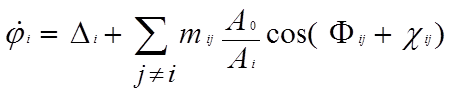(8)

где A_{i 0} – амплитуда колебаний i-го генератора в отсутствии связи, Φ_ij =φ_i – φ_j , (9)

Δ_i =ω_i – ω, (10)

m_ij = [(β_ij ⁽¹⁾ ω² – β_ij ⁽³⁾ )² + β_ij ⁽²⁾² ]^1/2 , (11)

(12)

Рассмотрим случай слабой связи между генераторами, когда в уравнениях для фаз (8) можно положить A_i =A_{i 0} . В синхронном режиме, когда , получим следующую систему уравнений для определения стационарных разностей фаз:

(13)

где i=1,2,...,N – 1, Δ_i,i+1 =ω_i – ω_i+1 =Δ_i – Δ_i+1.

Система уравнений (13) аналитически может быть решена лишь для частного случая полностью идентичных генераторов, когда A_{i 0} =A₀ , m_ij =m, χ_ij =χ, ω_i =ω для всех i и j. В этом случае уравнения (13) примут вид:

(i=1,...,N – 1).(15)

Уравнение (15) имеет два частных решения:

Φ_ij = 0, (16)

Φ_{i j} = ± (j – i) (17)

Частота синхронных колебаний в случае синфазного режима работы генераторов равна ω_с = ω + (N – 1)mcosχ, а во втором случае ω_с = ω – mcosχ [3].

8. 2. Пример: цепочка лазеров

Синхронизация в цепочке лазеров часто используется для получе­ния излучения большой интенсивности. Этого можно достигнуть, расположив лазеры в линию, так, что каждый взаимодействует с ближайшими соседями или со всеми другими лазерами. Добиться взаимодействия каждого лазера с остальными можно с помощью специального пространственного фильтра. При такой конфигурации каждый лазер взаи­модействует с остальными, но сила связи зависит от рас­стояния между лазерами. Результаты, представленные на рисунке 4, четко указывают на синхронизацию. Действительно, если бы лазеры были не синхронизованы, то излучение в дальней зоне представляло бы собой сумму некогерентных колебаний, и по­тому было бы пространственно однородным. Неоднородность распределения на рисунке 4 появляется из-за захвата фаз, это типичная интерференционная картина.

Рис. 4. Интенсивность излучения в дальней зоне при слабой связи лазеров.

9. Образование кластеров

9. 1. Кластеры в дискретной цепочке осцилляторов

Если в дискретной цепочке осцилляторы взаимодействуют очень слабо, то синхронизации не будет, и каждая система будет колебаться со своей частотой. При достаточно сильной связи будет наблюдаться синхронизация всей цепочки. В промежуточном случае можно ожидать появление частично синхронизированных режимов, с несколькими различными частотами. Поскольку связь стремится синхронизировать ближайших соседей, образуются кластеры синхронизированных осцилляторов [1].

Рис. 5. Зависимость наблюдаемых частот Ω_k от параметра связи ε в цепочке из пяти осцилляторов. Собственные частоты равны -1.8, -1.1, 0.1, 0.9, 1.9, функция связи выбрана в виде q(x)=sinx. С увеличением связи сначала осцилляторы 1 и 2 образуют кластер при ε≈ 0.4. Затем при ε≈ 0.6 появляется кластер из осцилляторов 4 и 5. При ε≈ 1.4 к нему присоединяется осциллятор 3. Наконец, при ε≈ 3 все осцилляторы синхронизируются.

9. 1. Кластеры в непрерывной колебательной среде

Образование кластеров в непрерывной колебательной среде является результатом двух противоположных факторов: неоднородности распределения собственных частот и связи, которая старается уравнять состоя­ния систем. Такая связь часто возникает вследствие диффузии, и поэтому называется диффузионной. Рассмотрим, что происходит на границе двух кластеров, имеющих разные частоты. Здесь важно различать случал дискретной цепочки и непрерывной среды.

В дискретной цепочке граница между двумя кластерами есть граница между двумя осцилляторами, имеющими разные частоты. Это просто означает, что они не захвачены: каждый колеблется со своей частотой. В отличие от этого, если в сплошной среде два ос­циллятора в двух пространственных точках имеют разные часто­ты, то между ними должен быть непрерывный переход. На пер­вый взгляд, можно просто провести непрерывный профиль частот, соединяющий эти точки. Более детальное рассмотрение показыва­ет, что это невозможно. Действительно, разные частоты отвечают разным скоростям вращения фазы. Поэтому разность фаз между точками, принадлежащими к двум кластерам, растет во времени со скоростью, пропорциональной разности частот. Следовательно, профиль фазы становится все более наклонным. С другой стороны, непрерывный крутой профиль фазы означает, что в среде образу­ются волновые структуры с все меньшей и меньшей длиной волны. Рост разности фаз между кластерами приводит к укорочению дли­ны волны со временем. Ясно, что этот процесс долго продолжаться не может — и действительно, среда находит выход из этой ситуации. Увеличивающийся градиент фазы уменьша­ется за счет пространственно-временного дефекта . Дефект обра­зуется, когда амплитуда колебаний обращается в ноль, он позволяет сохранить градиент фазы конечным.

Чтобы продемонстрировать, как возникает пространственно-временной дефект, предположим, что разность фаз между точка­ми 1 и 2, принадлежащими разным кластерам, достигла значения ≈2π. Если бы между 1 и 2 не было среды, то мы бы просто счи­тали состояния в этих точках почти идентичными. В среде, одна­ко, существует непрерывный профиль фазы между этими точками. Представляя как амплитуду, так и фазу в полярных координатах, мы можем изобразить поле окружностью. (рис. 6).