В соответствии с исходными данными комплексный коэффициент передачи системы в разомкнутом состоянии выглядит следующим образом:

,

где K_p1 (j w) – комплексный коэффициент передачи системы, Т – постоянная времени простого инерционного звена, входящего в систему в соответствии с заданием на работу.

Далее можно получить неравенство

,

где K_п – петлевой коэффициент передачи системы.

Отсюда получаем, К_ПГр равен

.

При подборе коэффициента передачи по третьему условию необходимо учитывать зависимость от него максимального значения ошибки слежения в переходном режиме, но для получения этой зависимости параметры системы должны быть известными, т.е. ее разработка в линейном приближении завершена, в том числе выполнен синтез цепей коррекции. Следовательно, должна быть завершена работа, требующая знания петлевого усиления. Поэтому здесь используется приближенная формула:

()

Примем коэффициент передачи K_п0 равным 50. Тогда с учетом заданного соотношения мощности сигнала к мощности помехи коэффициент передачи будет равен: .

Построим ЛАХ и ФЧХ системы. Логарифмическая амплитудно-частотная характеристика описывается следующим выражением:

, где .

Фазо-частотная характеристика определяется из равенства:

.

Логарифмическая амплитудно-частотная характеристика и фазо-частотная характеристики системы представлены в прил. 1.

Частота среза равна:

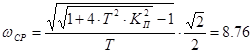(рад/с).

2. Коррекция системы

2.1 Анализ устойчивости системы по фазе

Запас устойчивости системы по фазе:

.

Полученный запас устойчивости по фазе не удовлетворяет требованиям задания на курсовую работу – запас устойчивости по фазе не меньше 30º. Исходя из этого необходимо включить в систему корректирующее звено, а именно форсирующее звено . Тогда передаточная функция системы примет вид:

.

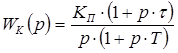Положим τ = 0.08 с. Далее для оценки влияния корректирующего звена необходимо построить логарифмическую амплитудно-частотную и фазо-частотную характеристики. Логарифмическая амплитудно-частотная характеристика данной системы будет описываться выражением:

, где .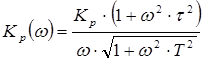

Фазо-частотная характеристика определяется из равенства:

.

Логарифмическая амплитудно-частотная характеристика и фазо-частотная характеристики системы с корректирующим звеном представлены в прил. 2.

Частота среза равна: