По полученным результатам можно сделать вывод, что среднеквадратическое отклонение ошибки слежения удовлетворяет требованиям задания на курсовую работу, поскольку оно (а точнее его квадрат) не превосходит 20% полуапертуры (0.2Δ f = 1000 Гц ), следовательно, нет необходимости в дополнительно коррекции системы.

3. Исследование срыва слежения

Для расчёта минимального значения отношения мощности сигнала и помехи q² _{mi n} по критерию равенства вероятности срыва слежения Р_ср = 0,05 за время слежения 1000 с в данной курсовой работе используется метод теории выбросов. В соответствии с ним вероятность срыва слежения отождествляется с вероятностью пересечения изображающей точкой границы апертуры дискриминатора – вероятностью выброса реализации за пределы апертуры дискриминатора. При использовании ряда допущений, справедливых при малых вероятностях срыва слежения, значение последней может быть найдено из приближенного равенства

,

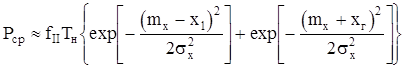где m_x – математическое ожидание ошибки слежения, – дисперсия ошибки слежения линеаризованной системы,

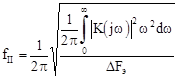– среднеквадратичное значение полосы пропускания следящей системы с коэффициентом передачи К ( j w) в замкнутом состоянии.

Линеаризованная дискриминационная характеристика дискриминатора описывается крутизной S_Д , равной K_П , и представлена на рис. 6.

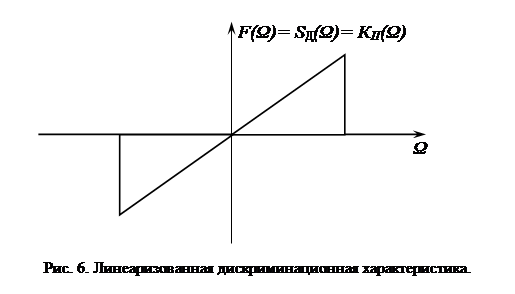
Следующие математические выкладки необходимы для получения зависимости вероятности срыва слежения о величины отношения мошности сигнала и шума.

Граница апертуры:

Ошибка слежения F определяется из соотношения:

(Гц).

Эквивалентная спектральная полоса помехи:

.

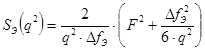Шумовая полоса системы:

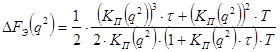, где

Среднеквадратичная полоса пропускания замкнутой системы с коэффициентом передачи K (j w):

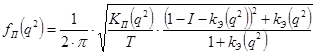, где .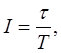

Дисперсия ошибки слежения линеаризованной системы и математическое ожидание ошибки слежения:

.

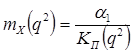Вероятность срыва слежения:

.

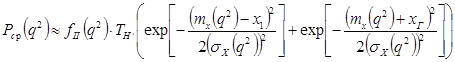В связи с тем, что зависимость вероятности срыва слежения от отношения q² мощностей сигнала и помехи имеет сложный характер, непосредственное вычисление q² _мин , соответствующего заданному значению P_ср , возможно применением численных методов решения алгебраических уравнений высокого порядка. В данной работе такое уравнение решается графическим методом.

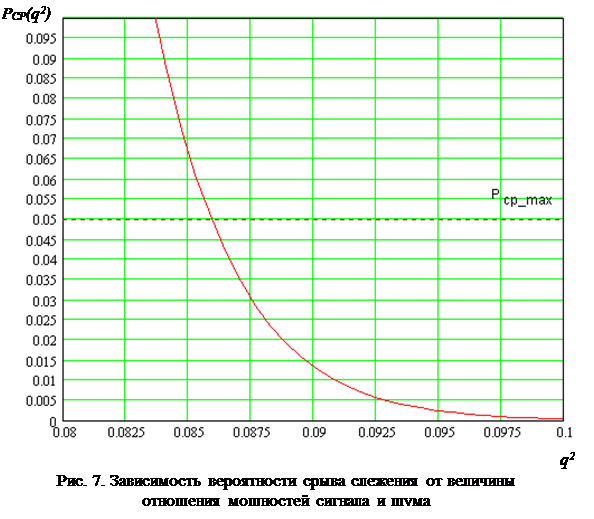
По графику определяем .

Заключение

В данной курсовой работе были рассчитаны основные параметры системы ЧАП. Параметры системы удовлетворяют показателям качества, оговоренным в задании на курсовую работу. Рассчитанная система обладает следующими свойствами: коэффициент петлевого усиления K_П0 = 50. С учетом того, что на входе действует помеха, К_П = 46,87 . При этом динамическая ошибка слежения X_Д = 200 Гц , что меньше, чем максимально допустимое значение 250 Гц . В систему введена цепь коррекции – форсирующее звено с постоянной времени τ = 0.08 с. Необходимость ведения корректирующего звена была вызвана тем, что исходная система не удовлетворяла требованиям устойчивости, оговорённым в задания на курсовую работу (запас устойчивости по фазе – не меньше 30º ). В результате коррекции система имеет следующие параметры: дисперсия ошибки слежения -7.3 Гц , запас устойчивости по фазе 42,27º. По результатам расчета можно составить структурную схему системы АПЧ:

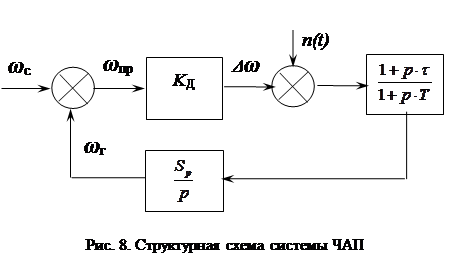
Библиографический список

1. Астрельцов Д.В. Системы радиоавтоматики: методические указания к выполнению курсовой работы по дисциплине «Теория управления и радиоавтоматика» – Екатеринбург: Издательство УГТУ, 1997 – 36 с.

2. Стандарт предприятия. Общие требования и правила оформления дипломных и курсовых проектов (работ). СТП УГТУ-УПИ 1-96. Екатеринбург, 1996.