Курсовая работа: Система частотной автоподстройки
Исходя из этого, запас устойчивости по фазе определяется как:
![]() .
.
Таким образом, путём введения в систему корректирующего (в данном случае форсирующего) звена удалось обеспечить требуемый запас устойчивости по фазе (согласно заданию на курсовую работу запас устойчивости по фазе должен быть не менее 30º).
2.2 Расчёт среднеквадратического отклонения ошибки слежения
Зависимость ошибки слежения от времени является случайным процессом, если, по крайней мере, одно из воздействий на систему является случайным процессом. Чаще всего таким воздействием является помеха, поступающая в приемное устройство в сумме (аддитивной смеси) с полезным сигналом, за изменениями одного или нескольких параметров которого следит разрабатываемая система. Указанная помеха может быть внутренним шумом приемного устройства или внешней помехой как естественного, так и искусственного происхождения. Чаще всего в реальных ситуациях помеха является суммой внутреннего шума приемного устройства и разнообразных процессов, источниками которых могут быть космические объекты (шумы космоса, солнца), земная поверхность (тепловое излучение поверхности земли, строений и сооружений), разнообразные промышленные и транспортные установки, генераторы радиосигналов, использующиеся в других радиосистемах, в том числе и специально созданных для противодействия разрабатываемой системе.
Задача помехоустойчивости – обеспечение нормальной работы системы в присутствии радиопомех – главным образом решается дискриминатором путем использования временной, частотной и пространственной селекции полезного сигнала при его приеме в присутствии помех. Однако, как указывалось выше, рациональное использование сглаживающих цепей также может принести ощутимый вклад в повышение помехоустойчивости системы.
Для расчета дисперсии ошибки, вызванной действием помех, необходимо знание статистического эквивалента дискриминатора – его дискриминационной и флуктуационной характеристики. Первая является зависимостью математического ожидания напряжения на выходе дискриминатора от ошибки слежения, а вторая – зависимостью интенсивности помехи на выходе дискриминатора от ошибки слежения. В целом напряжение на выходе дискриминатора UД ( t) имеет вид:
Uд (t) = F(x) + n(t),
где Х – ошибка слежения, n( t) – помеха на выходе дискриминатора, F( x) = < Uд ( t)>| x – условное математическое ожидание напряжения UД ( t) при фиксированном Х( t).
При небольших вариациях D x( t) ошибки слежения относительно динамической xд ( t), можно записать:
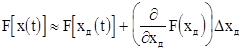 ,
,
где ![]() при
при ![]() – коэффициент передачи (крутизна характеристики) дискриминатора в точке x=xд .
– коэффициент передачи (крутизна характеристики) дискриминатора в точке x=xд .
При изменениях динамической ошибки xд (t) коэффициент передачи дискриминатора также является функцией времени. В случае приблизительно постоянной динамической ошибки или при нахождении всей ошибки x(t) на линейном участке дискриминационной характеристики можно полагать Кд постоянной величиной.
Тогда для расчета дисперсии флуктуационной составляющей ошибки слежения можно воспользоваться частотным методом
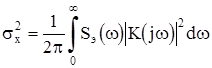 ,
,
где Sэ ( w) = Sn ( w)/ KД 2 – спектральная плотность мощности помехи n( t), пересчитанной на вход дискриминатора (спектральная плотность эквивалентной помехи),
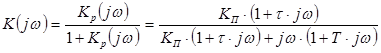
– комплексный коэффициент передачи замкнутой следящей системы.
При слабой зависимости Sэ ( w) от частоты w в пределах полосы пропускания замкнутой следящей системы можно полагать ![]() , вынести ее из под интеграла и получить:
, вынести ее из под интеграла и получить:
sх 2 » Sэ ×DFэ где Sэ =Sn (0)/KД 2 , 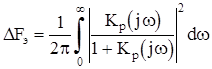 – эквивалентная шумовая полоса линеаризованной следящей системы.
– эквивалентная шумовая полоса линеаризованной следящей системы.
Вычисление интеграла в равенстве можно выполнить, используя формулы, приведенные в учебнике [3]. Подынтегральное выражение в можно представить в виде квадрата модуля дробно-рациональной функции
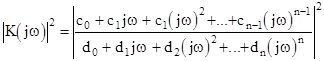 .
.
В этом случае результат интегрирования зависит от значений коэффициентов cк и dк , а также от порядка системы n . Для систем второго порядка в [3] приведено выражение:
![]() для n=2.
для n=2.
Для
![]() следует, что с0 = КП , с1 = КП τ, d0 = KП , d1 = (1 + KП τ), d0 = Т. Таким образом:
следует, что с0 = КП , с1 = КП τ, d0 = KП , d1 = (1 + KП τ), d0 = Т. Таким образом:
![]() (Гц).
(Гц).
Выражение для шумовой полосы имеет вид ![]() (Гц). Тогда спектральная плотность эквивалентной шумовой помехи равна:
(Гц). Тогда спектральная плотность эквивалентной шумовой помехи равна:
![]() .
.
Исходя из этого, можно определить среднеквадратическое отклонение ошибки слежения: