Курсовая работа: Система кількісних оцінок ступеня ризику

або ж

(2.17)

W = M(|X ? Mo(X)|).

Слід мати на увазі, що даний підхід до оцінки ризику застосовується у випадку, коли економічний показник може мати як позитивний, так і негативний інгредієнт (тобто Х = Х^± ).

При абсолютному вираженні міри ризику під час прийняття економічних рішень широко використовується дисперсійний підхід.

Дисперсією (варіацією) V(X) випадкової величини Х є зважена щодо ймовірності величина квадратів відхилення випадкової величини Х від її математичного сподівання М(Х). Дисперсія характеризує міру розсіяння випадкової величини Х навколо М(Х) і обчислюється за формулою:

(2.18)

V(X) = M(X – M(X))² = M(X² ) – (M(X))² .

Для дискретної випадкової величини

(2.19)

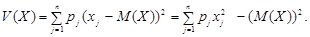
Середньоквадратичним (стандартним) відхиленням випадкової величини Х називається величина

(2.20)

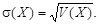
Підхід до оцінки ризику, що спирається на варіацію чи середньоквадратичне відхилення, вважається класичним. Причому чим більшими будуть ці величини, тим більшим буде ступінь ризику, пов’язаного з певною стратегією, тобто величина ризику

(2.21)

W = V(X) або W = s (X).

Слід зазначити, що такий підхід до оцінки ступеня ризику використовується, коли Х = Х^± .

Слід мати на увазі, що при класичному визначенні міри ризику однаково трактуються як додатні, так і від’ємні відхилення величини реального ефекту від сподіваної величини, тобто виконується гіпотеза про те, що коливання випадкової величини Х (прибутку, ЧПВ, збитків) в обидві сторони однаково небажані. Але у ряді випадків це не так і цю гіпотезу доводиться відкидати.[4.67]

Якщо випадкова величина Х = {x₁ ; …; x_n } відображає прибутки (Х = Х⁺ ) і значення х_i < M(X) (оцінка прибутку х_і є реалізацією випадкової величини Х і є меншою від сподіваної величини прибутку), то це є ознакою несприятливої ситуації. В той же час додатне відхилення вказує на те, що реалізація випадкової величини (прибутку) є більшою, ніж сподівана величина, і це для менеджера (інвестора) є, очевидно, кращою, тобто сприятливою ситуацією.

(2.22)

(2.24)

? ???????????? ?????? ???????????? ?????? ???????? ? ????, ?? ????? ?????????? ???? ? ?????????????? ??? ????????? (?????????) ???????? ? ??? ???? ?????????? ????????? ????? ?? ????? ???? ???????????? ?????????? ??? ?????????? ????????. [2.231] ??? ????? ? ?????? ???? ?????? ???????????????? ???? ????????, ??? ???????????? ?? ????????:

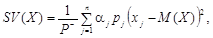
де 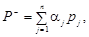a_j — індикатор несприятливих відхилень, який визначають за формулою:

(2.23)

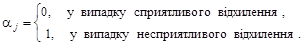
Якщо ж, наприклад, Х = {x₁ ; …; x_n } відображає можливі варіанти збитків (Х = Х ^– , тобто має негативний інгредієнт), то

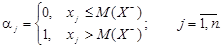
Для неперервної випадкової величини Х відповідно:

(2.25)

(2.26)

(2.27)

? ?????????? ????? ???? ???????? (?????? ?? ????? ?????????? ???????) ????????????? ???? ??????????? ??????????.

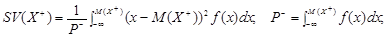
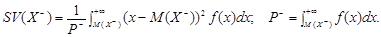
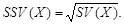
Згідно із сказаним вище чим більшою буде величина SV(X) (чи SSV(X)), тим більшим буде ступінь ризику,

(2.28)

(2.29)

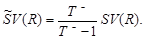
Для оцінки ризику можна використовувати також середньоквадратичне відхилення від зваженого середньо геометричного:

(2.30)

,

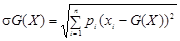
або ж оцінку цієї величини на основі статистичних даних:

(2.31)

.

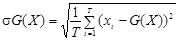
Виявляється, що портфель цінних паперів, сформований на підставі максимізації зваженої середньо геометричної норми прибутку, характеризується найвищою очікуваною вартістю в кінці середньо - та довготермінового періоду (найвищим кінцевим багатством).

З точки зору неокласичного підходу до оцінки ризику доцільним є впровадження такого показника ступеня ризику, як семі квадратичне відхилення від зваженого середньо геометричного випадкової величини [11.156]:

(2.32)

,

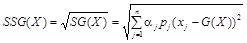
де SG(X) — величина семі варіації по відношенню до зваженого середньо геометричного SSG(X) — семі квадратичне відхилення, a_j — індикатор j-го несприятливого відхилення.

Оскільки величина SG(X) має негативний інгредієнт, то, як і раніше, ризик вважається більшим при більших значеннях SG(X) (чи SSG(X)).

3. Ризик у відносному вираженні

3.1 Коефіцієнт сподіваних збитків