Курсовая работа: Система передавання неперервних повідомлень із використанням широтно–імпульсної модуляції

За даною схемою, особливості визначення завадостійкості передавання неперервних повідомлень включають такі особливості:

1. оцінюється вірогідність прийняття рішення у найскладнішій задачі приймання, а саме задачі фільтрування (відновлення переданого повідомлення із спотвореного шумами спостережуваного сигналу;

2. корисними перетвореннями неперервних повідомлень на сигнали і навпаки у процесі передавання є модуляція і демодуляція, а тому по суті оцінюється завадостійкість способу модуляції і демодуляції є й інші корисні та паразитні перетворення від виходу модулятора до входу демодулятора, які впливають на якість фільтрування.

Перелічені особливості передавання неперервних повідомлень призводять до того, що ускладнюється розв’язання задачі синтезу оптимальних приймачів і оцінки їх завадостійкості. Тому конкретні задачі оптимального приймання ставлять так, щоб використати накопичений досвід і результати, отримані при визначенні завадостійкості системи передавання дискретних повідомлень.

2. АНАЛІЗ СТАТИСТИЧНИХ ХАРАКТЕРИСТИК І ПАРАМЕТРІВ ПЕРЕДАВАЄМОГО ПОВІДОМЛЕННЯ

За умовою курсової роботи вихідне безперервне повідомлення являє (зображає) собою стаціонарний гаусовский випадковій процес з нульовим математичним чеканням ( , де М – знак статистичного усереднення по безлічі реалізації), потужність і функція кореляції якого задані в табл. 1.

Гаусовский (нормальний) випадковий процес у будь - який момент часу характеризується одномірної ФПВ наступного (такого) виду:

(2.1)

В часовій і спектральній областях стаціонарний випадковий процес визначається, відповідно, функцією кореляції і спектральній щільності потужності чи енергетичним спектром , де . . Ці характеристики зв'язані парою перетворень Вінера - Хінчина:

(2.2)

(2.3)

Враховуючи, що для стаціонарного випадкового процесу обидві ці функції дійсні і парні, тоді відношення (2.2 і 2.3) можливо записати у такому вигляді:

(2.4)

(2.5)

Функція кореляції згідно з вихідними даними має такий вигляд:

(2.6)

Тепер підставимо відомі величини у формулу (2.6)

(2.7)

По (2.7) побудуємо графік функції кореляції:

Рис. 2.1 – Функція кореляції

Тепер згідно (2.4) розрахуємо спектр щільності потужності повідомлення:

(2.8)

Побудуємо графік спектра щільності потужності повідомлення згідно з виразом (2.8)

Рис. 2.2 – Спектр щільності потужності повідомлення

По функції знаходимо енергетичну ширину спектра , за формулою (2.9):

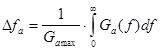(2.9)

де - максимальне значення енергетичного спектру.